【CS2】Ch06 Survival models 生存模型
本文介绍生存模型，属于CS2第六章的内容，也是学习CM1的寿险精算部分的先修内容。
本文不仅适用于英国精算师的考试，Jackie 在写这篇推文时也参考了北美体系的内容，所以考SOA的同学也不妨看一下。
Notation
\((x)\) 表示当前为 \(x\) 岁的个体，\(T_{x}\)表示(x)的余命的随机变量(Future lifetime rv.)，\(T_{0}\) 为新生儿的余命的随机变量。\(K_{x}\)表示 \((x)\) 的取整余命的随机变量(Curtate future lifetime rv.)。
\(T_{0}\)的分布
cdf of \(T_{0}\):
\[F_{0}(x)=P(T_{0}\leq x)\]
sf of \(T_{0}\):
\[S_{0}(x)=P(T_{0}> x)=1-F_{0}(x)\]
pdf of \(T_{0}\):
\[f_{0}(x)=\frac{d}{dx}F_{0}(x)=-\frac{d}{dx}S_{0}(x)\]
Relationship between \(T_{0}\) and \(T_{x}\)
Events that are equivalent (important relationship between \(T_{0}\) and \(T_{x}\)): \[ T_{x}\leq t \Leftrightarrow T_{x}=T_{0}-x \leq t| T_{0}>x \]
\(T_{x}\)的分布
cdf of \(T_{x}\):
\(F_{x}(t)=P(T_{x}\leq t)=\frac{F_{0}(x+t)-F_{0}(x)}{1-F_{0}(x)}\)
sf of \(T_{x}\):
\(S_{x}(t)=P(T_{x}> t)=1-F_{x}(t)=\frac{S_{0}(x+t)}{S_{0}(x)}\)
pdf of \(T_{x}\):
\(f_{x}(t)=\frac{d}{dt}F_{x}(t)=\frac{f_{0}(x+t)}{S_{0}(x)}\)
Chaining Survival
\[S_{0}(x+t)=S_{0}(x)S_{x}(t)\] \[S_{x}(t+u)=S_{x}(t)S_{x+t}(u)\]
Conditions on \(S_{x}(t)\)
\[S_{x}(0)=P(T_{x}> 0)=1\] \[\lim\limits_{x\to \infty}S_{x}(t)=\lim\limits_{x\to \infty}P(T_{x}> t)=0\] \(S_{x}(t)\) is non-increasing in \(t\)
Assumptions on \(S_{x}(t)\)
\(S_{x}(t)\) is differentiable \(\forall t > 0\)
\[E[T_{x}]< \infty\] \[Var[T_{x}]< \infty\]
The force of mortality
\(\mu_{x}\)，称为force of mortality, hazard rate, transition intensity, 定义为： \[ \begin{aligned} \mu_{x}&=\lim\limits_{dx\to 0^{+}}\frac{P(T_{0}\leq x+dx|T_{0}>x)}{dx}\\\\ &=\lim\limits_{dx\to 0^{+}}\frac{P(T_{x}\leq dx)}{dx} \end{aligned} \] 需要掌握的几个公式： \[ \mu_{x}=\frac{f_{0}(x)}{S_{0}(x)}=-\frac{\partial}{\partial x}log S_{0}(x) \]
\[ \mu_{x+t}=\frac{f_{x}(t)}{S_{x}(t)}=-\frac{\partial}{\partial x}log S_{x}(t) \]
\[ S_x(t)=exp{(-\int_{0}^{t}\mu_{x+r}dr)} \]
Typical \(\mu_{x}\) curve for humans
\(\mu_{x}\) on \(log_{10}\) scale (ELT15 (Males) Mortality Table) The main features of \(\mu_{x}\) are:
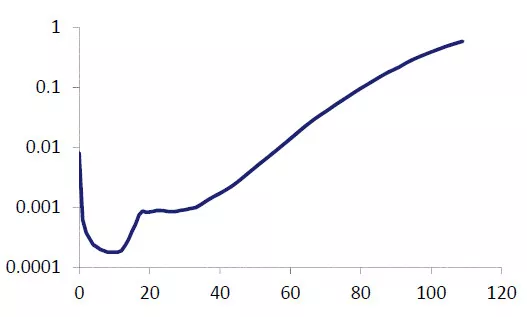
- High infant mortality
- An ‘accident hump’ at ages around 20
- The nearly exponential increase at older ages
Some Common Mortality Models
- Exponential Model: Constant force of mortality
- De Moivre Model: \(T_{x}\sim Uni(0,\omega-x)\)
- Compertz Model
- Generalized (or Modified) De Moivre Model
Actuarial Notation
Survival:
\[\px{t}{x}=P(T_{x}> t)=S_{x}(t)\]
Mortality:
\[\qx{t}{x}=P(T_{x}\leq t)=F_{x}(t)\]
Deferred Mortality:
\[\qx{t|u}{x}=P(t < T_{x}\leq t+u)\]
It's convention that \(t=1\) year, we omit the 1, i.e.
\(\px{1}{x}=\px{}{x}\), \(\qx{1}{x}=\qx{}{x}\), \(\qx{t|1}{x}=\qx{t|}{x}\).
3 ways to calculate \(\qx{t|u}{x}\)
\[\qx{t|u}{x}=F_{x}(t+u)-F_{x}(t)=\qx{t+u}{x}-\qx{t}{x}\] \[\qx{t|u}{x}=S_{x}(t)-S_{x}(t+u)=\px{t}{x}-\px{t+u}{x}\] \[\qx{t|u}{x}=\px{t}{x}\cdot \qx{x+t}{u}\]
Relationship between F and f
\[ \qx{t}{x}=\int_{0}^{t} \px{u}{x}\mu_{x+u}du \]
Approximate \(q_{x}\) with \(\mu_{x+u}\)
For small \(q_{x}\):
\[ \begin{aligned} q_{x}\approx \int_{0}^{1}1\cdot \mu_{x+u}du\approx \mu_{x} \end{aligned} \]
\(q_{x}\) can also be approximated by \(\mu_{x+\tfrac{1}{2}}\).
Distributional Quantities of \(T_{x}\)
Mean of \(T_{x}\)
Complete expectation of life: \[ \mathring{e}_x=E[T_x]=\int_0^{\infty}tf_x(t)dt =\int_0^{\infty} t\cdot \px{t}{x}\actsymb{}{}{\mu}{}{x+t} dt =\int_0^{\infty}\px{t}{x}dt \]
Median of \(T_{x}\)
This is the value \(m\) s.t. \(P(T_{x}>m)=0.5\). i.e. \(\px{m}{x}=0.5\)
Variance of \(T_{x}\)
\[ Var T_x=E[{T_x}^2]-(E T_x)^2 \]
Distribution of \(K_{x}\)
pmf:
\[P(K_{x}=k)=P(k\leq T_{x}\leq k+1)=\qx{k|1}{x}=\qx{k|}{x}\]
cdf
\[P(K_{x}\leq k)=1-\px{k+1}{x}=\qx{k+1}{x}\]
sf:
\[P(K_{x}> k)=\px{k+1}{x}\]
Mean of \(K_{x}\)
\[ e_{x}=E[K_{x}]=\sum_{k=0}^{\infty}k \cdot P(K_{x}=k)=\sum_{k=1}^{\infty}\px{k}{x} \]
Variance of \(K_{x}\)
\[ Var[K_{x}]=2\sum_{k=1}^{\infty}k \cdot \px{k}{x}-e_{x}-(e_{x})^{2} \]
Relationship between \(e_{x}\) and \({\stackrel{o}{e}}_{x}\)
\[ \mathring{e}_x \approx e_x+\frac{1}{2} \]
正在检查 Disqus 能否访问...