西浦MTH214和利物浦MTH373期中考试前三章复习要点

Jackie

IFoACM1

发布于：2021年3月18日

次浏览

Multiple State Models、Joint life and last survivor benefit、 Pension三章的复习要点

今年一月份我辅导了十多位西浦和利物浦学生的寿险精算I课程（MTH217和MTH273），这学期是西浦的寿险精算II（MTH214），前几天也给几位学生辅导了MTH214的前两章，这里给大家总结一下MTH214期中考试要求的前三章：

Multiple State Models
Joint life and last survivor benefit
Pension

利物浦下学期要考MTH373的同学们也可以收藏一下，因为我在备课时已经结合了MTH373和MTH214的课件和真题。

Multiple State Models

多状态模型。在 IFoA CM1 的“Competing risks”一章的基础上（多状态模型概率的书写和计算，多状态模型保险金和保费的期望现值的积分式书写和计算，CFM假设下的多重减因模型和多重减因表的构建），还需要加上tpxiibar的求和式证明和tpx01积分式证明，UDD假设下的多重减因模型（UDD是2014年以前的CT5考察的内容，现在已经删除，虽然属于MTH214和MTH373的知识点，但是一般也不考），多状态模型下的准备金和多状态模型下的Thiele's differential equation书写。

需要注意在符号表示上的差别。首先是多状态模型中tpxij和muxij中对状态ij的习惯表示上，CM1中通常用字母表示状态，如tpxHS和muxSD；而MTH214和MTH373中习惯用数字表示状态，如tpx01和mux12 . 另外在多重减因模型的概率符号表示上也有不同。CM1用下图右侧的符号，MTH214和MTH373用左侧的符号。符号对照表如下：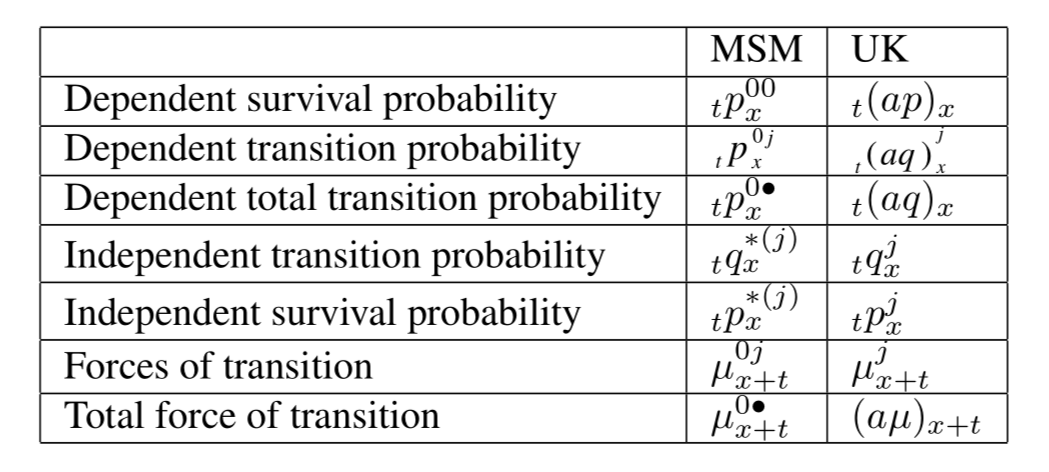

符号建议按照右侧一栏记忆，不容易混淆。

在考题风格上，多状态模型保险金和保费的期望现值的积分式书写和计算题型完全一致；多重减因概率计算上，MTH373的一道题目直接改编自CM1的真题；多重减因表题型，CM1主要考察转移力改变后重新构建多重减因表，而MTH214和MTH373中的多重减因表考得较为简单，主要考察离散型寿险的EPV计算。

Joint life and last survivor benefit

双生命函数部分。这部分和CM1考察的真题题型完全一致。具体地，对应CM1的以下三个章节：

Joint life and last survivor functions

主要题型为tpx:y, tpx:ybar, tqx:y, tqx:ybar这4类不带顺序的双生命死亡概率的计算，以及联合寿险，联合年金，最后生存人寿险，最后生存人年金的期望现值和方差的计算（主要有积分式求解和查表计算两类题型）。

Contingent and reversionary benefits

主要题型为nq:x(2):y等带顺序的双生命死亡概率的计算，或有寿险的期望现值和方差的计算（主要考积分式求解的题型，一般不考查表计算），继承年金的保险金和保费期望现值的计算（类似阅读理解题，需要根据题目灵活判断该继承年金的保险金责任，建议在掌握基础继承年金期望现值的积分式和查表式的基础上，理解六种复杂形式继承年金期望现值的积分式和查表式）。

Mortality profit

主要考察双生命死差益。这一章也和CM1的的“Mortality profit”一章的历年真题一致。因为单生命死差益题型已经在MTH217和MTH273中考察过，所以重点考双生命死差益题型。会涉及双生命准备金的计算。双生命题型一般只出last survivor的情况（因为joint life太简单），计算时对处于不同状态的保单需要分类计算其死差益，一般出要分三类的情况（所以要先计算三类不同的DSAR），最难（或者说是计算量最大）可以出到五类DSAR.