【知识点串讲】CM1 Survival models 生存模型

Jackie

IFoACM1

发布于：2021年1月18日

次浏览

CM1寿险精算部分的第一课。

开个新系列【知识点串讲】，本系列的文章会完全按照对应科目的考纲对知识点进行梳理。本文按照英国精算师考试CM1新考纲要求掌握的知识点来写，是寿险精算部分第一课时的内容。

人产生以后，人类也就像单个的人一样，从一种像本能一样固定不变的状态，而进入一种非确定的、偶然的自由状态。他只知道过去——至于未来，只能肯定是死亡。 ——弗洛姆《爱的艺术》

余命的随机变量

符号标记和定义

\((x)\) 表示当前为 \(x\) 岁的个体，我们用 \(T_{x}\) 和 \(K_{x}\) 表示余命的随机变量：

• \(T_{x}\) 表示 \((x)\) 的余命的随机变量（Future lifetime random variable），特别地，\(T_{0}\) 为新生儿（newborn）的余命的随机变量；
• \(K_{x}\) 表示 \((x)\) 的取整余命的随机变量(Curtate future lifetime random variable)，\(K_{x}\) 是 \(T_{x}\) 的整数部分，即：\(K_{x}=[ T_{x}]\).

先讲 \(T_{x}\) 的分布的定义：

• \(T_{x}\) 的累积分布函数（Cumulative Distribution Function, cdf）：\(F_{x}(t)=P(T_{x}\leq t)\)

• \(T_{x}\) 的生存函数（Survival Function, sf）：\(S_{x}(t)=1-F_{x}(t)=P(T_{x}\geq t)\)

• \(T_{x}\) 的概率密度函数（Probability Density function, pdf）：\(f_{x}(t)=\dfrac{d}{dt}F_{x}(t)\)

要推导 \(T_{x}\) 的分布，首先需要写出 \(T_{0}\) 的分布。

\(T_{0}\)的分布

• cdf of \(T_{0}\): \(F_{0}(x)=P(T_{0}\leq x)\)

• sf of \(T_{0}\): \(S_{0}(x)=P(T_{0}> x)=1-F_{0}(x)\)

• pdf of \(T_{0}\): \(f_{0}(x)=\frac{d}{dx}F_{0}(x)=-\frac{d}{dx}S_{0}(x)\)

\(T_{0}\) 和 \(T_{x}\) 的关系

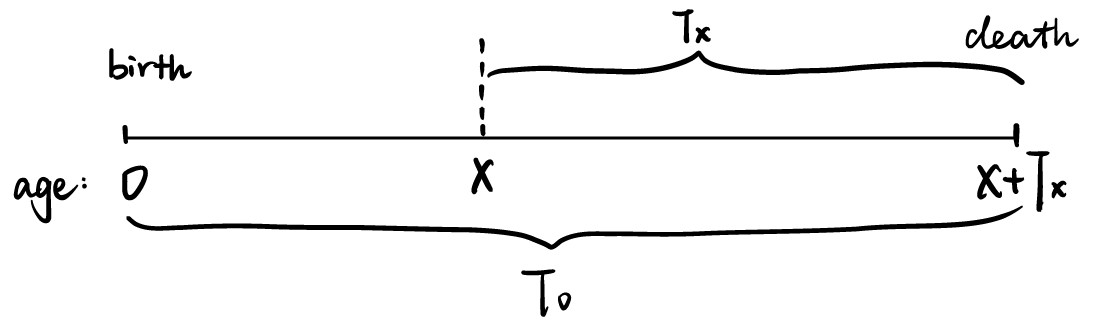
以下两个事件是等价的（ equivalent）： \[ T_{x}\leq t \Leftrightarrow T_{x}=T_{0}-x \leq t| T_{0}>x \]

根据这个关系式，可以通过 \(T_{0}\)的分布推导 \(T_{x}\) 的分布。

\(T_{x}\)的分布（用\(T_{0}\)的分布表示）

• cdf of \(T_{x}\): \(F_{x}(t)=P(T_{x}\leq t)=\frac{F_{0}(x+t)-F_{0}(x)}{1-F_{0}(x)}\)

• sf of \(T_{x}\): \(S_{x}(t)=P(T_{x}> t)=1-F_{x}(t)=\frac{S_{0}(x+t)}{S_{0}(x)}\)

• pdf of \(T_{x}\): \(f_{x}(t)=\frac{d}{dt}F_{x}(t)=\frac{f_{0}(x+t)}{S_{0}(x)}\)

Chaining Survival

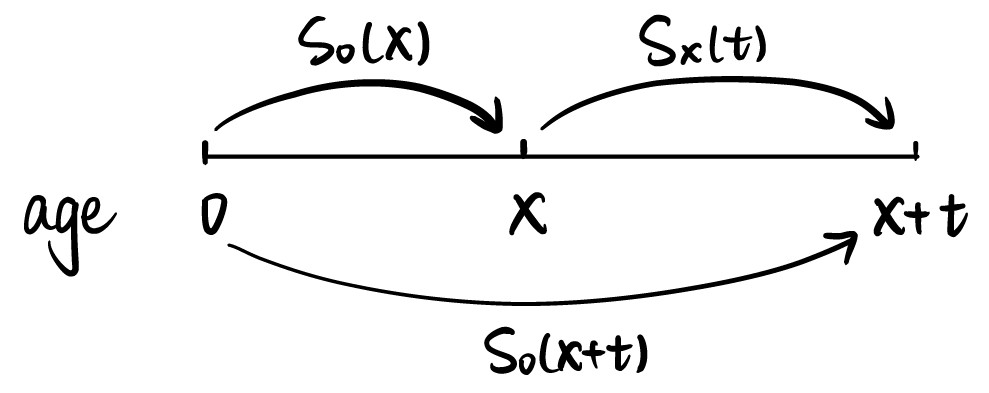
\[S_{0}(x+t)=S_{0}(x)S_{x}(t)\]

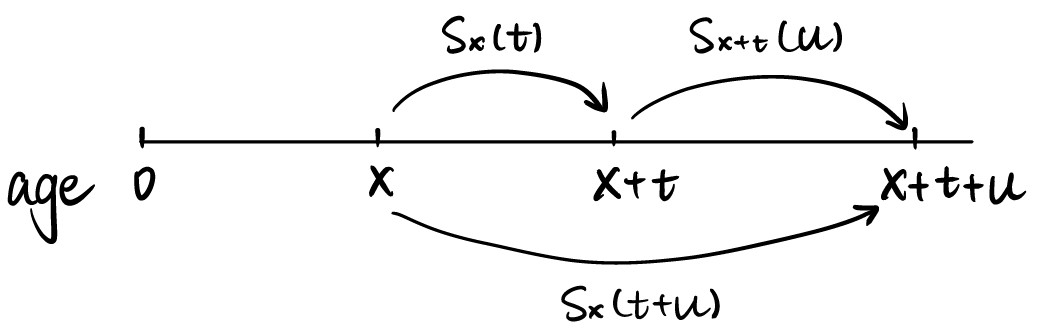
\[S_{x}(t+u)=S_{x}(t)S_{x+t}(u)\]

精算标记

为便于表示余命的分布，我们用 \(p\) 概率和 \(q\) 概率来作为它们在精算中的标记（actuarial notation）。

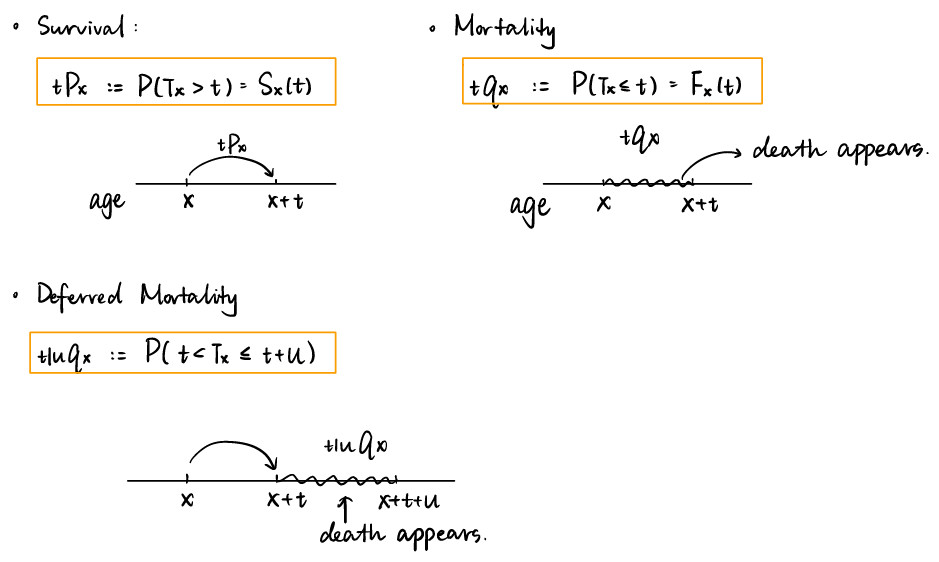
• Survival: \(\px{t}{x}=P(T_{x}> t)=S_{x}(t)\)
• Mortality: \(\qx{t}{x}=P(T_{x}\leq t)=F_{x}(t)\)
• Deferred Mortality: \(\qx{t|u}{x}=P(t < T_{x}\leq t+u)\)

当 \(t=1\) 时，符号中的1可以这样省略： \(\px{1}{x}=\px{}{x}\), \(\qx{1}{x}=\qx{}{x}\), \(\qx{t|1}{x}=\qx{t|}{x}\).

前面对于 \(S_{x}(t)\) 和 \(F_{x}(t)\) 成立的公式对于\(\px{t}{x}\) 和 \(\qx{t}{x}\) 同样成立：

• \(\px{t+u}{x}=\px{t}{x}\cdot \px{u}{x+t}=\px{u}{x}\cdot \px{t}{x+u}\)
• \(\qx{t+u}{x}=1-\px{t}{x} \times \px{t}{x+u}=1-(1- \qx{u}{x})(1- \qx{t}{x+u})\)

3种计算 \(\qx{t|u}{x}\) 的方法

• \(\qx{t|u}{x}=F_{x}(t+u)-F_{x}(t)=\qx{t+u}{x}-\qx{t}{x}\)
• \(\qx{t|u}{x}=S_{x}(t)-S_{x}(t+u)=\px{t}{x}-\px{t+u}{x}\)
• \(\qx{t|u}{x}=\px{t}{x}\cdot \qx{u}{x+t}\)

分布函数 \(F\) 和概率密度函数 \(f\) 的关系

\[ \qx{t}{x}=\int_{0}^{t} \px{u}{x}\mu_{x+u}du \]

死亡力

\(\mu_{x}\)，称为 force of mortality, hazard rate, transition intensity, 定义为： \[ \begin{aligned} \mu_{x}&=\lim\limits_{dx\to 0^{+}}\frac{P(T_{0}\leq x+dx|T_{0}>x)}{dx}\\\\ &=\lim\limits_{dx\to 0^{+}}\frac{P(T_{x}\leq dx)}{dx} \end{aligned} \]

\(\mu_{x}\)可以理解为\((x)\)在极短的时间\(dx\)内死亡的“极限概率”（注意，不是概率），或者说瞬时的死亡率。\(\mu_{x}\)是 rate，而不是 probability。

用 \(T_{0}\) 的分布表示 \(\mu_{x}\)

\[ \mu_{x}=\dfrac{f_{0}(x)}{S_{0}(x)} =-\frac{1}{S_{0}(x)} \cdot \frac{d}{d_{x}} S_{0}(x) =-\frac{\partial}{\partial x} \log S_{0}(x) \]

用 \(T_{x}\) 的分布表示 \(\mu_{x+t}\)

\[ \mu_{x+t}=\frac{f_{x}(t)}{S_{x}(t)}=-\frac{\partial}{\partial x}log S_{x}(t) \]

\[ \px{t}{x}=S_x(t)=exp{(-\int_{0}^{t}\mu_{x+r}dr)} \]

用 \(\mu_{x+t}\) 表示概率密度函数 \(f_{x}(t)\)

\[ f_{x}(t) =-\frac{d}{d t} S_{x}(t) =\mu_{x+t}\cdot \px{t}{x} \]

典型的人类死亡力曲线

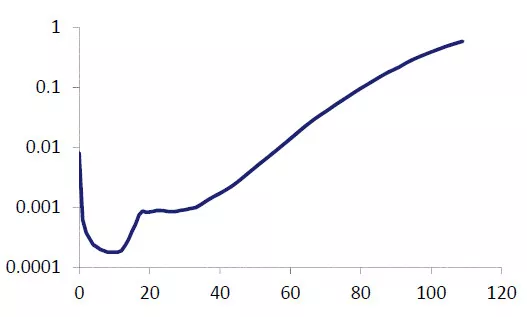
The main features of \(\mu_{x}\) are:

• High infant mortality
• An ‘accident hump’ at ages around 20
• The nearly exponential increase at older ages

余命随机变量的分布特征

\(T_{x}\) 的分布特征

Mean of \(T_{x}\)

完全余命的期望（Mean ）： \[ \mathring{e}_x=E[T_x]=\int_0^{\infty}tf_x(t)dt =\int_0^{\infty} t\cdot \px{t}{x}\actsymb{}{}{\mu}{}{x+t} dt =\int_0^{\infty}\px{t}{x}dt \]

Median of \(T_{x}\)

\(T_{x}\)的中位数（Median）为使得 \(P(T_{x}>m)=0.5\)的 \(m\)，即： \(\px{m}{x}=0.5\)

Variance of \(T_{x}\)

\(T_{x}\)的方差（Variance）： \[ Var[T_{x}]=E[T_{x}^{2}]-(E[T_{x}])^{2} \]

\(K_{x}\) 的分布特征

\(K_{x}=[T_{x}]\)，也就是说，\(K_{x}\)代表complete/full years of future life for \((x)\)的整数部分。

注意，如果终极生存年龄（limiting age） \(w\) 和个体 \((x)\)的年龄 \(x\) 均为整数，那么 \(K_{x}\) 的范围为 \(\{0, 1, 2, \ldots , w-x-1\}\).

• pmf:\(P(K_{x}=k)=P(k\leq T_{x}\leq k+1)=\qx{k|1}{x}=\qx{k|}{x}\)

• cdf: \(P(K_{x}\leq k)=1-\px{k+1}{x}=\qx{k+1}{x}\)

• sf:\(P(K_{x}> k)=\px{k+1}{x}\)

Mean of \(K_{x}\)

取整余命的期望： \[ e_{x}=E[K_{x}]=\sum_{k=0}^{\infty}k \cdot P(K_{x}=k)=\sum_{k=1}^{\infty}\px{k}{x} \]

Variance of \(K_{x}\)

\[ Var[K_{x}]=2\sum_{k=1}^{\infty}k \cdot \px{k}{x}-e_{x}-(e_{x})^{2} \]

\(e_{x}\) 和 \(\mathring{e}_x\) 的联系

\[ \mathring{e}_x \approx e_x+\frac{1}{2} \]

本页文档最后更新于：2021年3月30日