【CT1】币值加权收益率 MWRR 和时间加权收益率 TWRR

Jackie

IFoACM1

发布于：2021年1月18日

次浏览

币值加权收益率 MWRR 和时间加权收益率 TWRR 的计算，以及线性插值法的使用。

MWRR为币值加权收益率，TWRR为时间加权收益率。MWRR和TWRR是旧大纲CT1的Measurement of investment performance一节的内容，新大纲CM1中已经删去。但在2019年的慕再精算竞赛中有考察，且在西浦 MTH120 和利物浦 MATH267 科目中仍是一道必考题，值得一看。

MWRR:Money-weighted rate of return

注意，在币值加权收益率MWRR中，用到的只是“new money”（新投入的钱，而不是基金本身运转得到的钱）

用以下公式计算出的 \(i\) 即为MWRR： \[ F_{0} (1+i)^{T}+C_{t_{1}} (1+i)^{T-t_{1}}+C_{t_{2}} (1+i)^{T-t_{2}}+\cdots+C_{t_{n}} (1+i)^{T-t_{n}}=F_{T} \]

其中，\(F_{0}\) 是0时刻的 fund value；\(F_{T}\) 是 \(T\) 时刻的 fund value.

计算MWRR时，用一阶近似找到近似的\(i\)（用 \(1+ni\) 代替 \((1+i)^n\)），再比这个 \(i\) 大和比这个 \(i\) 小分别找两个 \(i_{1}\) 和 \(i_{2}\)，再用线性插值法算出更为准确的 \(i\).

TWRR:Time-weighted rate of return

时间加权收益率TWRR是通过以下式子算出的\(i\)：

\[ (1+i)^{T}=\frac{F_{t_{-}}-}{F_{0}+C_{0}} \frac{F_{t_{2}-}}{F_{t_{1}-}+C_{t_{1}}} \frac{F_{t_{3}-}}{F_{t_{2}-}+C_{t_{2}}} \cdots \frac{F_{T}}{F_{t_{n}-}+C_{t_{n}}} \]

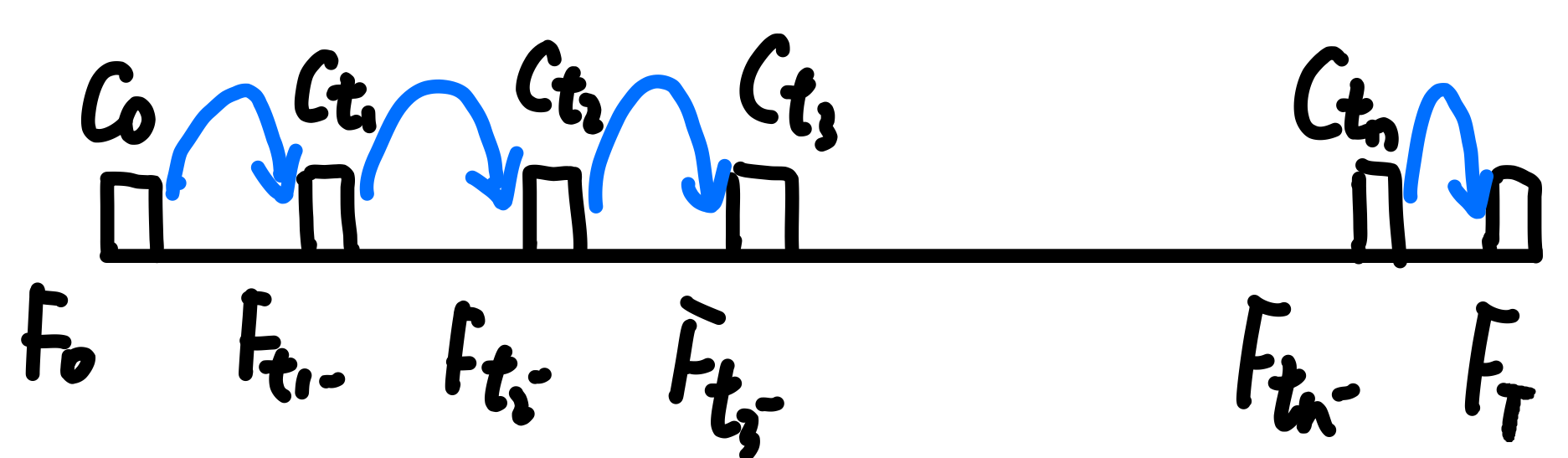
TWRR的原理：计算“没有任何事情发生的时间区间里的”growth factor.

Linked internal rate of return

\[ (1+i)^{t_{n}} ={(1+i_1)}^{t_1} (1+i_{2})^{t_{2}-t_{1}} (1+i_{3})^{t_{3}-t_{2}} \ldots(1+i_{n})^{t_{n}-t_{n-1}} \]

线性插值法

假定我们在利率\(i_{1}\) 和 \(i_{2}\) 下计算出的现值分别为 \(P_{1}\)和\(P_{2}\) ， 我们希望计算出准确的现值\(P\)对应的利率\(i\).

可以用下图表示：

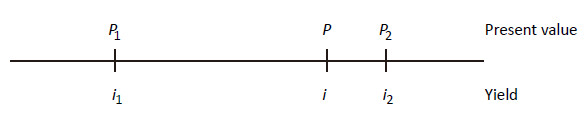
\[ \frac{i-i_{1}}{i_{2}-i_{1}}=\frac{P-P_{1}}{P_{2}-P_{1}} \]

可以解出\(i\)的值为: \[ i \approx i_{1}+\frac{P-P_{1}}{P_{2}-P_{1}} \times\left(i_{2}-i_{1}\right) \]

本页文档最后更新于：2023年12月17日

利息理论