IFoA 英国精算师考试 CT4 精算模型的学习大纲,备考必看。各章的主干知识点和考点总结。
CT4分为两部分,1-6章为随机过程,7-13章为生存模型。
随机过程部分
Chapter 1 Principles of actuarial modelling
精算建模的原则。是简单的介绍性质的章节。
熟悉概念即可。比如随机模型(stochastic models)和确定性模型(deterministic models)的优缺点,建模的基本步骤等。
Chapter 2 Stochastic processes
介绍了随机过程的基本概念,随机过程的种类(根据state和 time是离散还是连续的),白噪声(White noise),随机游走(random walk),平稳性(Stationarity),弱平稳性,独立增量(Independent increments)等。也是简单的介绍性质的章节。
Chapter 3 Markov chains
马尔可夫链。占25%的分值。大概会出两题,每题12-13分。
给定一个马尔可夫链的实例,要能画出马尔科夫状态转移图(transition graph),进而对其分析。掌握The Chapman-Kolmogorov equations。
Chapter 4 The two-state Markov model
两状态的马尔可夫链。本章是第五和第六章的基础章节。
要掌握两状态马尔可夫链的三个基本假设。并由此推导公式:
\[ \px{t}{x}=exp(-\int^t_0 \mu_{x+s}ds) \]
掌握在两状态模型中的,死亡力的极大似然估计量。
Chapter 5 Time-homogeneous Markov jump processes
时齐带跳的马尔可夫过程。比较难。
首先,要注意转移力(transition rates)和转移概率(transition probabilities)的区别。
要求根据实例写出转移矩阵(transition matrix)。
HSD model(health-sickness-death model)的图像非常重要,后续的很多例子都基于此。
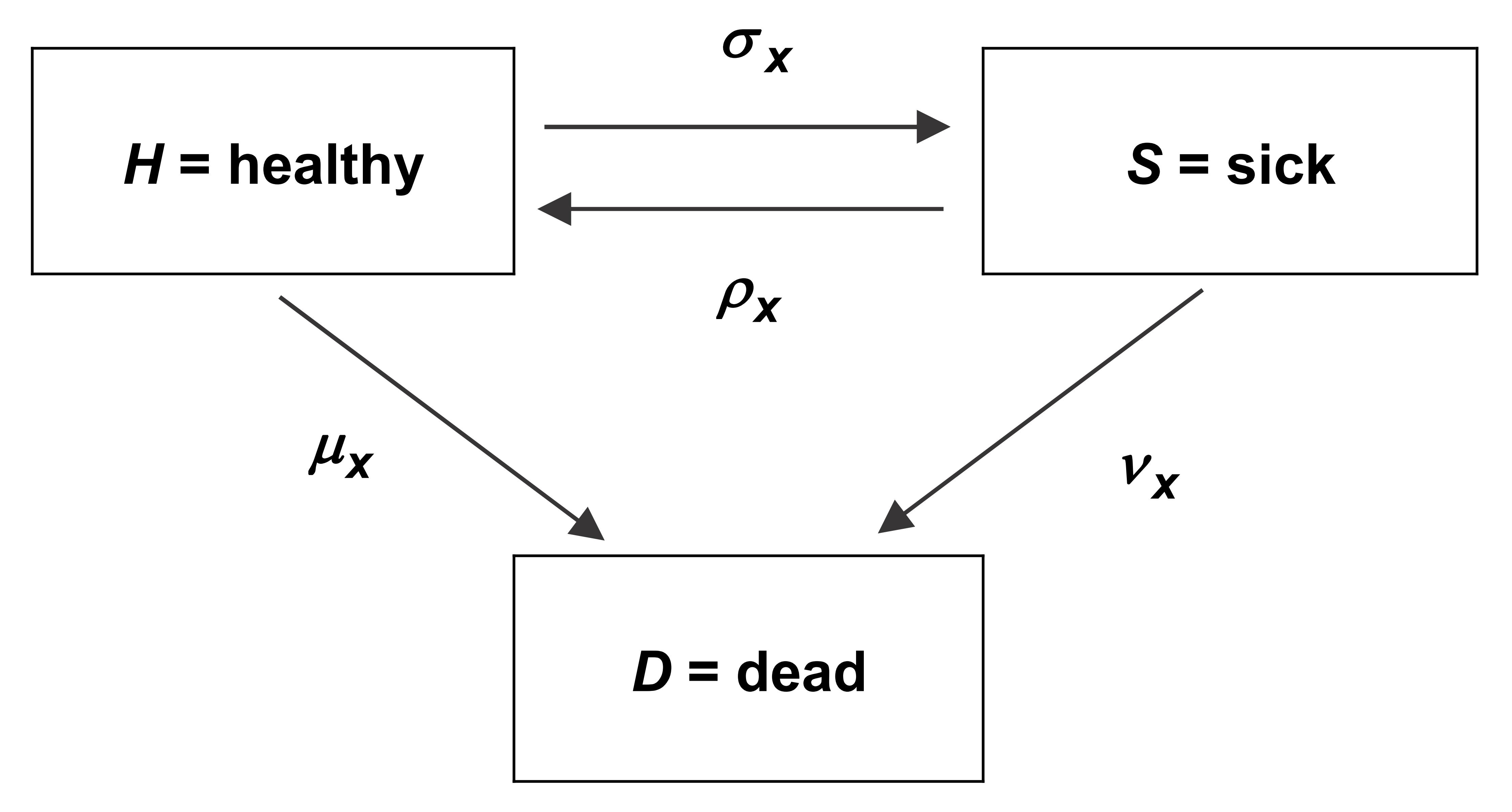
要掌握 Kolmogorov 的前后差分方程。掌握 Holding time(也叫 waiting time,等待时间),occupancy probabilities(占据(某状态的)时间),状态间转移的期望时间(Expected time to reach state \(k\) starting from state \(i\))的计算。
简单的二重减因模型(simple two-decrement model)的两个公式要会推导。
\[ p_{01}(x, x+t)=\frac{\mu_{01}}{\mu_{01}+\mu_{02}}\left[1-e^{-\left(\mu_{01}+\mu_{02}\right) t}\right] \]
\[ p_{02}(x, x+t)=\frac{\mu_{02}}{\mu_{01}+\mu_{02}}\left[1-e^{-\left(\mu_{01}+\mu_{02}\right) t}\right] \]
Chapter 6 Time-inhomogeneous Markov jump processes
非时齐带跳的马尔可夫过程。有些难。多数真题出10分,有一张卷子里是20分。
非时齐与时齐的区别在于,它的转移力不再是一个常数,而是一个与时间有关的函数。称作with duration dependence。
生存模型部分
Chapter 7 Survival models
生存模型。
这一章和CT5存在重叠,主要介绍了余命(Future lifetime)的分布函数,生存概率,死亡概率,死亡力(The force of mortality),取整余命的期望(Curtate expectation of life)的基本概念,简单的参数生存模型(Simple parametric survival models),两个死亡力法则(The Gompertz and Makeham laws of mortality)
Chapter 8 Estimating the lifetime distribution function
估计 lifetime distribution。很简单。
和上一章的参数估计方法不同,本章介绍的KM和NA生存分析法都是非参数估计方法(nonparametric approach to estimation)。非参数估计没有对生存函数的分布做预先的假定,因而更加准确。
主要掌握Kaplan-Meier (or product limit)生存分析法和Nelson-Aalen生存分析法,以及两者计算得到的估计量之间的联系。
要注意实际数据一定是存在删失或者截尾的。在生存分析中考虑了这一点。
Chapter 9 Proportional hazards models
比例风险模型。很简单。9分。
比例风险模型中的hazard,即是指死亡力。
较为常用的是The Cox proportional hazards model。要求能够指出baseline的实际情景,并在题中给定情景下通过对协变量(covariates)的取值计算hazard。看几道例题就很清楚了。
Chapter 10 The Binomial and Poisson models
二项模型和泊松模型。偏理论的章节。泊松模型是两者中较好的。一般不直接考察这一章节,但这一章有助于对下一章的理解。
要掌握 Actuarial estimate 和 Poisson estimate 的计算。
Chapter 11 Exposed to risk
风险暴露数。分为中心风险暴露数和初始风险暴露数。
要掌握两者的精确计算和数据存在删失时的近似估计。要注意,census data 和 death data 在 age 的定义上必须是一致的。
年龄有三种定义方法:
aged \(x\) last birthday:上一个生日的年龄为 \(x\)
aged \(x\) next birthday:下一个生日的年龄为 \(x\)
aged \(x\) nearest birthday:最近的一个生日的年龄为 \(x\)
由年龄的定义方法得到的某年龄 \(x\) 处在的实际年龄区间称作 Rate interval。

Chapter 12 Graduation and statistical tests
修匀和统计方法。统计方法的部分在CT3中已经学过。
Chapter 13 Methods of graduation
介绍了三种修匀方法。graduation by parametric formula,graduation by reference to a standard table,graphical graduation
结语
CT4 最重要的概念是死亡力。CT4中的每一章都是和死亡力相关的,无论是直接或者间接。Force of mortality,transaction rates,比例风险模型中的hazard,这些都是指死亡力。
You have three methods of graduation, but only one way to pass the exam——work hard.