让死亡率曲线Duang的一下光滑起来。
大家都知道一般我们从数据中做出来的对死亡率的最佳估计是非平滑的,大概就是这样的曲线:
但是我们一般想要做出需要平滑完整的曲线,像下图: 
从非平滑的曲线到平滑完整的过程,叫做死亡率的修匀(Graduation)。
Graduation的核心有两点:
- 对曲线进行平滑
- 外推(Extrapolation): 需要估计数据点之外的死亡率。比如数据只到了80岁,我们需要把80到100岁的死亡率也预估出来。
实务操作有很多简化的办法,比如计算移动平均等等。
18年SoA发布了一篇实际中如何用统计方法来实现Graduation的指南,A Practitioner’s Guide to Statistical Mortality Graduation。这个方法很多和英国CMI用的方法是一样的。这篇文章给大家总结一下摘要。文章的数据是基于CPM2014男性的数据集。
介绍
寿险的发生率一般由两部分组成,一部分是Baseline rate,一部分是Improvement Trend (死亡的发生率降低,轻重疾发生率恶化)。
在开始之前呢,我们先定义一下什么样的模型是好的模型。 - 模型应该能达到需要的预测准确性。 - 模型应该用尽量少的假设,并且每一个建模过程中的决定都应该好好地记录下来。
方法一
死亡率随着年龄的增长是指数型的。因此我们可以对于死亡率取Log之后,用直线进行拟合。
如果我们对每个年龄的中心死亡率(大约是某年龄段死亡人数/某年龄段的总人数)做统计,那么数据图如下:
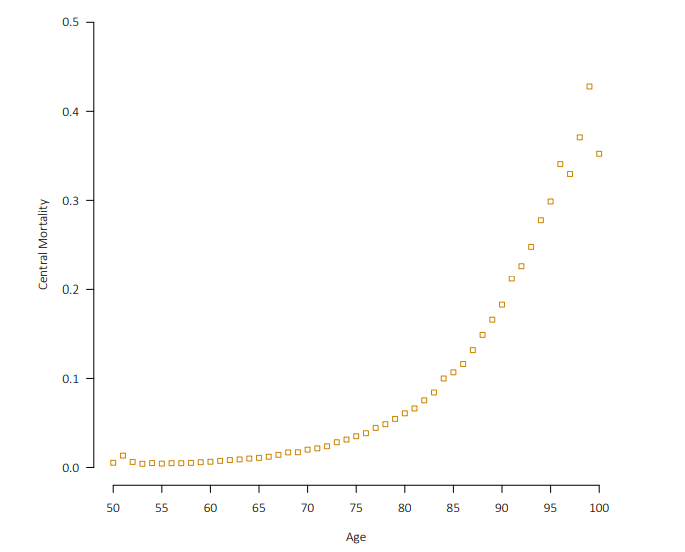
取Log后数据如下: 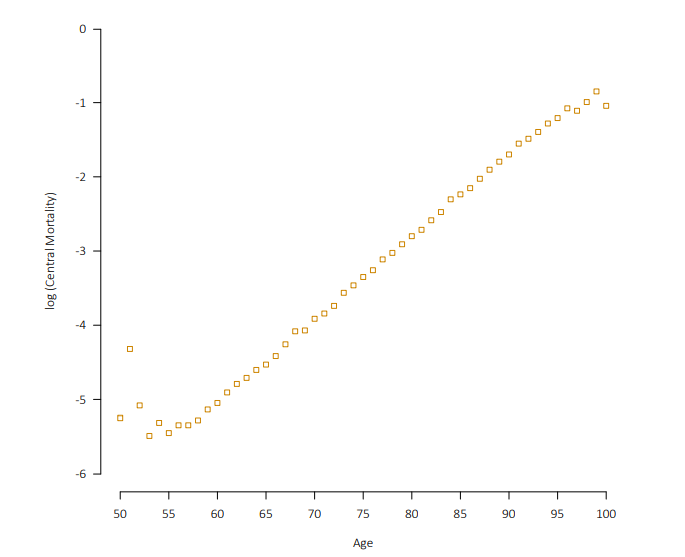
可以看出,这个模型虽然简单,但是能很好地捕捉数据的特征。 但是这个模型存在局限性,就是它没有考虑到信度的问题。-- 死亡人数多(或总人数多)的年龄死亡率计算可靠性更高,死亡人数少(或总人数少)的年龄死亡率计算可靠性更低。
解决这个问题有一个简单粗暴的方式,那就是使用Weighted Least Square——以不同年龄段的暴露数进行加权,然后进行最小平方距离估计。不过我们下面要讲的是一些更基于数学公式原理的方法。
方法二
为了弥补这个缺点,我们有了方法二。那就是假设每个年龄段的死亡人数呈现泊松分布,然后利用最大似然估计来计算参数值。 假设每个年龄段死亡人数为\(D_x\),死亡概率为\(m_x\),年龄为\(x\)的人数为\(E_x\) 那么:
\[Dx \sim Poisson(E_x\hat{m_x}) \]
假设每个年龄段的死亡人数相互独立。如果我们把每个观察值出现的概率相乘,就得到了所有观察值同时出现的概率。最大化这个概率我们就能得到相关最佳估计参数。
假设\(m_x\)取决于某个参数\(\theta\),那么Log-likelihood function如下:
\[l(\theta ) = \sum_x[-E_x\hat{m}_x(\theta) +d_xlog(E_x\hat{m}_x(\theta))-log(d_x\!)]\]
由于\(log(d_x\!)\)与\(\theta\)不相关,所以在这个最大化\(\theta\)的问题中可以去掉。只需要最大化:
\[ \sum_x[-E_x\hat{m}_x(\theta) +d_xlog(E_x\hat{m}_x(\theta))]\]
可以看出,对于\(E_x\)和\(d_x\)越大的观察值对这个最大化问题的影响会更大一些。
假设\(m(\theta)\)是和x之间存在log-linear的关系,那么上面的式子可以写为:
\[l(\alpha,\beta ) = \sum_x[-E_xe^{\beta x+\alpha} +d_xlog(E_xe^{\beta x+\alpha})]\]
求\(\alpha\)和\(\beta\)的最优解的问题。
对\(m(\theta)\)和\(x\)之间log的关系进行拓展
在方法一和方法二中,我们都假设死亡率和年龄之间呈现指数增长的关系。这和Gompertz在1825年提出的死亡率法则是一致的。(死亡率法则:\(\mu_x = e^{\alpha + \beta x}\))
我们常常说死亡率会随着年龄指数型增长,如果究其根本要找出可以这样讲的一个源头来的话,那么就会是Gompertz的这个法则。但是需要提出的是,死亡率会随着年龄指数型增长的这个说法并不完全准确。后人对这个死亡力随着年龄变化的形式进行了改进,我们之后再讲。
虽然这个死亡率是对死亡强度\(\mu_x\)做出的假设,这里我们直接把这个法则用于\(m_x\)上,最后的结果差别不大。
Makeham在1860和1867年对这个死亡率假设进行了改进,他们加入了一个常数来更好地抓住中年死亡率的特征。
\[\mu_x = e^ {\epsilon}+ e^{\alpha + \beta x}\]
注: \(\epsilon\)是常数
Perks在1932年对Makeham的公式做出了拓展。拓展的方式是用\(\mu_x = e^ {\epsilon}+ e^{\alpha + \beta x}\)替换logistic函数的x。这个死亡力的公式分别在1959和2012年又被Beard和Richards做出了改变。最终得出的形式如下:
\[\mu_x = \frac{e^ {\epsilon}+ e^{\alpha + \beta x}}{1+ e^{\alpha + \rho + \beta x}}\]
但是模型并非越复杂越好,模型更复杂了之后到底是否更多地抓住了死亡率曲线的特征,还需要进一步探究。从下图可以看到,比起基础的Gompertz模型,它的拓展形式更好地抓住了低年龄和高年龄的死亡率变化特征:
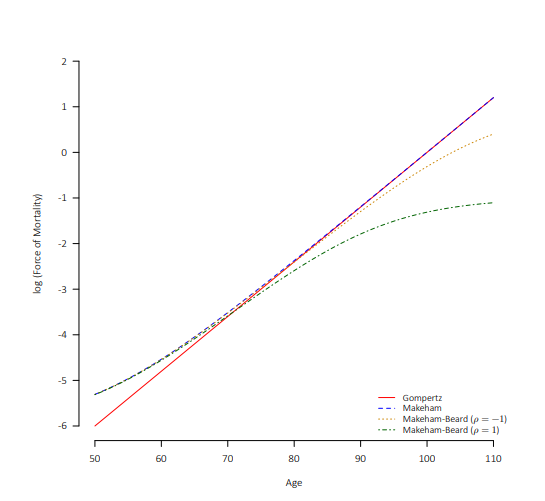
然而,如果你对上面的几种形式还不满足,那么可以考虑一个更加拓展的形式\(GM(r,s)\)
\[\mu_x = GM(r,s) = \sum_{i=0}^{r-1}a_ix^i + e^{\sum_{j =0}^{s-1}b_jx^j}\]
下表总结了不同的死亡力假设。

对低年龄死亡率和高年龄死亡率的拓展
除了对死亡率曲线进行平滑外,我们很多时候还需要把死亡率曲线向高年龄和低年龄进行拓展。原因是在这些年龄段我们的经验数据较少。这个时候用方法一中的Log-linear就是不太好的,因为Log-linear相对来说没有捕捉到高年龄死亡率变化的特征。
从低年龄的经验数据向高年龄死亡率拓展有以下的几种办法。
- 用Logistic Extension拟合数据 -- 类似于上面讲到的Perks或者Beard的死亡力模型。用这个模型的好处就是这两个模型可以自然捕捉高年龄和低年龄段死亡率的特征。
- 用多项式的形式进行拟合。
- 让死亡率逐渐趋近于人群死亡率(国家统计数据)这种方法的基础应该是在这篇帖子https://www.actuarygarden.com/topic/132中提到的Compensation law of mortality。
- 利用极限值理论(Extreme Value Theory)
相比于用低年龄的死亡率向高年龄的死亡率拓展而言;向低年龄的死亡率拓展显得更加困难。有时候甚至他们不适用于一类人群。
比如说,如果要用正常年龄领取年金的人(大于65岁)预计50-60岁领取年金的人的死亡率就是不合适的。因为50-60岁就开始领年金的人,和50-60岁还在工作的人比起来,一般健康情况会更差一些。这种情况下,用另外一个死亡表估计他们的死亡率也许会更好。
下图是领取年金的人的死亡率和普通雇员的死亡率的对比。可以看到,领取年金的人的死亡率在50-60岁的区间的趋势和60岁之后的趋势明显不同。还在工作的雇员则死亡率更低一些。
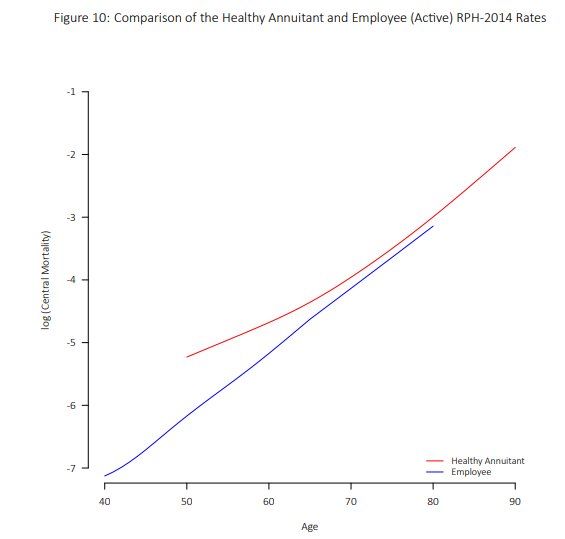
如果真的要向用高年龄死亡率的数据向更低年龄的死亡率预估的话,那么可以使用Makeham定理的一些版本以及\(GM(r,s)\)拓展拟合。有的时候某些多项式拟合也能取得不错的效果。
对这篇文章的分享就到这里,如果有兴趣的话呢,可以看看原文更加丰富的内容。原文中还有R代码的实现。可以一试或者和我讨论。