介绍精算的R包:actuar
今天我们来介绍一个专为精算设计的R包: Actuar.
参考的文献是Journal of Statistical Software 08年的文章 actuar: An R Package for Actuarial Science
这个包能够涵盖四个精算中常用的功能:
- 损失分布建模 (Loss distribution modelling)
- 风险理论 (Risk theory)
- 复合层次模型 (Compound hierarchical models)
- 信度理论 (Credibility theory)
接下来,我们就一步步来看每个功能是如何被实现的~
损失分布建模
分布拓展
精算师需要对不同的损失分布进行建模,R基础包已经包含了常见分布的概率密度函数(probability
density function (pdf)), 累积分布函数(cumulative distribution function
(cdf)) 以及分位数函数(the quantile function),在R中分别用d,
p, q, r加上分布名称简写组成。
Base R支持的分布以及其分布简写分别为 - beta: beta -
binomial: binom - Cauchy: cauchy -
chi-squared: chisq - exponential: exp - Fisher
F: f - gamma: gamma - geometric:
geo - hypergeometric : hyper - logistic:
logis - lognormal: lnorm - negative binomial:
nbinom - normal: norm - Poisson:
pois - Student t: t - uniform:
unif - Weibull: weibull
在此基础上,actuar包在两个方面进行了拓展。第一个方面是对支持的损失分布进行了拓展,如图为拓展的分布
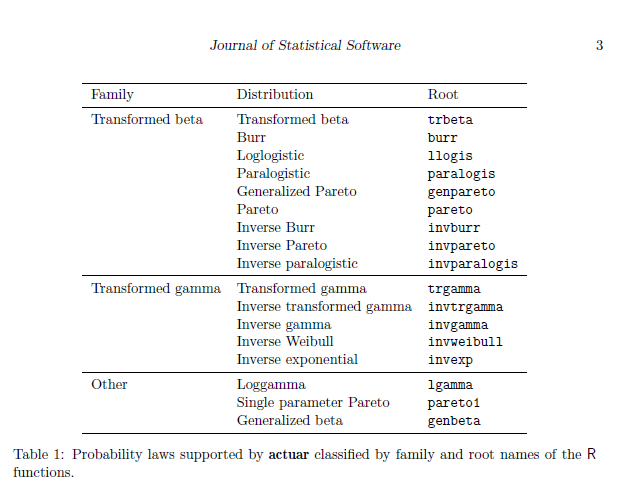
其中root这列就是调用函数的时候需要用到的名称简写,例如生成随机服从Loggamma分布的序列,则需要写
rlgamma(n, shapelog, ratelog)
第二个方向的拓展是增加了可以应用于分布上的函数,不仅限于d,
p, q, r, actuar还支持theoretical
raw moment / theoretical limited moment / the moment generating function
的计算,但是这些计算仅支持部分分布,除了actuar包拓展的分布外,还包含部分Base
R中的分布(beta, exponential, chi-square, gamma, lognormal, normal
(不支持lev), uniform 和 Weibull ),以及SuppDists中的分布inverse
Gaussian - theoretical raw moment: \(E(X^k)\)。在R中用m调用。 -
theoretical limited moment: \(E(min(X,
x)^k)\)。在R中用lev调用。 - moment generating
function: \(E(e^{tX})\)。在R中用mgf调用。
分组数据
分组数据简单的来说就是每个区间和每个区间对应的频数
| Group | Frequency (Line 1) | Frequency (Line 2) |
|---|---|---|
| (0; 25] | 30 | 26 |
| (25; 50] | 31 | 33 |
| (50; 100] | 57 | 31 |
| (100; 150] | 42 | 19 |
| (150; 250] | 65 | 16 |
| (250; 500] | 84 | 11 |
actuar包允许用户输入分组数据,并对分组数据进行求平均数,可视化等处理。
在数据量大,处理单个数据时比较慢的时候,这个功能的用处比较大。
数据集
actuar包中内置了数据集“dental"。这是一个精算数据集,包含了牙科疾病的独立数据(individual
data)和分组数据(groupped data)。 用法 1
2data("dental")
data("gdental")
计算经验矩(Empirical moments)
actuar包提供了两个进行矩估计的函数。
第一个是emm。这个函数可以计算基于经验的k阶矩。用到的数据集既可以是独立数据(individual
data),也可以是分组数据(groupped data)。 用法 1
2
3
4# 注意,dental和gdental是刚刚提到的包自带数据集。order参数既可以是数字也可以是Array.
emm(dental, order = 1)
emm(gdental, order = 1)
emm(dental, order = c(1,2,3))
第二个函数是elev这个函数用来计算经验分布的有限期望值(empirical
limited expected
value)。什么叫做有限期望值呢?举个例子,在保险中假设某保险公司只承保100w以下的损失,也就是承保损失的分布为\(\min(100w,
Loss)\)。那么如果求承保损失分布的期望,期望就是有限期望,且极限是100w。
用法为 1
2
3lev<-elev(dental)
#注意这里的1,000,000是刚刚提到的极限,可以换成任何你想计算的值
lev(1000000)
最小距离估计
两个最常用来拟合模型的参数估计方法(参数估计是假设数据呈现某种分布的情况下,用数据去估计这个分布的参数是什么。)是最大似然估计(Maximum Likelihood)和最小距离估计(Minimum Distance)。
MLE最常用的包是MASS中的fitdistr。这里不多做介绍。Actuar为第二种方法提供了一个函数mde,和fitdistr的用法类似。
最小距离估计,顾名思义,就是找到让理论分布和实际分布“距离”最近的参数。mde支持三种定义方式。
第一种定义是Cramer-von Mises method (CvM),最小平方距离,也就是我们常说的最小二乘法。这种方法既适用于独立数据(individual data),也可以用于分组数据(groupped data)。
但是另外两种方法The modified chi-square method (chi-square)和layer average severity method (LAS)只能用于分组数据。
用法如下,参数是 - gdental:数据集, -
pexp:用拟合的分布的分布函数(F),这里选择的是Exponential
Distribution的分布函数, -
measure:我们刚刚说到的三种方法,可以选择"CvM", "chi-square" 和 "LAS"
1
mde(gdental, pexp, start = list(rate = 1/200), measure = "CvM")
保险范围调整分布计算(Coverage modifications)
保险保障一般都有免赔额和限额,因此Actuar包提供了计算有免赔额/限额情况下损失分布的函数。 只要知道原本分布的pdf或者cdf,就可以得到免赔额/限额情况下损失分布的pdf或者cdf。
风险理论
在风险聚合模型中,我们假设个体的风险损失金额分布和发生损失的个体数分布是独立的,从而计算出总体分布的数值cdf。
在计算总体分布的过程中,我们常常需要做的一个操作是把损失金额分布的连续分布离散化。离散化就是把连续分布\(f(x)\)的定义域分成很多小段,用每小段\(f(x)\)的上界/下界/中间值来代表新生成的分布在这个区间的值。
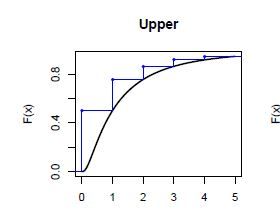

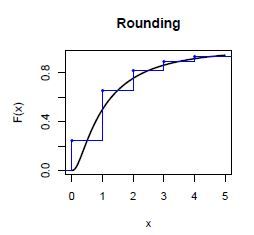
离散化的语法如下
1 | fx <- discretize(pgamma(x, 2, 1), method = "upper", from = 0, to = 17, step = 0.5) |
参数解释 - pgamma(x, 2, 1): 用来离散化的连续函数的pdf - method = "upper":离散化的方法,我们上面讲到了"upper", "lower"和"rounding",另一个没有讲到的是"unbiased"。 - from = 0, to = 17:离散化函数的定义域 - step = 0.5:离散化定义域分成的小区间的范围
有了离散化的损失金额分布,接下来就可以计算总体损失分布了。aggregateDist这个函数提供了五种计算总体损失分布的办法。这五种方法大多数都需要损失金额分布是离散分布。可以用上面的discretize把连续分布离散化后再计算总体损失分布。
这几种方法分别是 - Recursive calculation - Exact calculation by numerical convolutions - Normal approximation of the cdf - Normal Power II approximation of the cdf - Simulation of a random sample from S and approximation of FS(x) by the empirical cdf 这里不做过多介绍,想了解的小伙伴可以参照原文。
aggregateDist的用法例子如下
1 | Fs <- aggregateDist("recursive", model.freq = "poisson", model.sev = fx, lambda = 10, x.scale = 0.5) |
参数解释 - "recursive":总体损失分布计算方法,可选“recursive", "convolution", "normal", "npower", "simulation", - model.freq = "poisson":发生理赔的频数分布,这里用了Poisson, - model.sev = fx:发生理赔的金额损失分布,注意要是离散分布, - lambda = 10:Poisson分布的lambda - x.scale = 0.5:Severity分布的单位。比如说如果Severity单位是每1000元,这里就写1000
连续时间破产模型
根据我们学习的连续时间破产理论,终极破产概率遵从下面的不等式
\(\psi (u)\leq e^{-\rho u}\)
其中\(\rho\)也叫做adjustment
coefficient。Actuar包提供了adjCoef这个函数帮助我们计算adjustment
coefficient。用法如下:
假设每两个理赔发生时间间隔(服从参数为2的指数分布)和理赔大小(服从参数为1的指数分布)相互独立,费率为2.4,那么\(\rho\)的计算如下: 1
adjCoef(mgf.claim = mgfexp(x), mgf.wait = mgfexp(x, 2), premium.rate = 2.4, upper = 1)
破产概率
Actuar包提供了ruin这个函数来帮助我们计算任意初始盈余下的破产概率。
理赔金额分布和理赔发生时间间隔分布可以在“exponential”, "Erlang"和"phase-type"之间选择。选择后需要在下一个函数参数写相应分布的参数值。如果提供了"weights"这个参数,那么选择的分布是“exponential”或者"Erlang"混合分布。
下面是一个例子 1
ruin(claims = "p", par.claims = list(prob = prob, rates = rates), wait = "e", par.wait = list(rate = c(5, 1), weights = c(0.4, 0.6)))
复合层次模型(Compound Hierarchical Models)
复合层次模型是风险聚合模型(Collective risk
model)中的频率模型(Frequency)或者损失金额模型(Severity)有层次结构。层次结构一般指的是模型的参数也服从某一个分布的模型。
下面是一个复合层次模型的实例 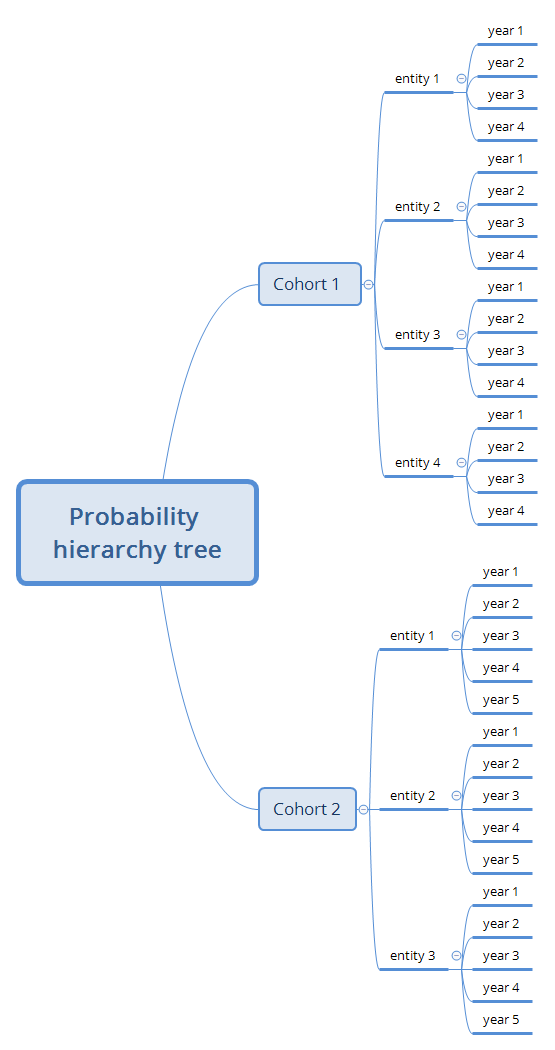
其中每层的分布都取决于前一层的分布。比如说保险损失在哪一年取决于它属于哪个entity,
在哪个entity又取决于在哪个Cohort。在下面的例子中,损失的频率和大小都服从这种层次分布
代码用例如下 1
2
3
4
5nodes <- list(cohort = 2, entity = c(4, 3), year = c(4, 4, 4, 4, 5, 5, 5))
mf <- expression(cohort = rexp(2), entity = rgamma(cohort, 1), year = rpois(weights * entity))
ms <- expression(cohort = rnorm(2, sqrt(0.1)), entity = rnorm(cohort, 1), year = rlnorm(entity, 1))
wijt <- runif(31, 0.5, 2.5)
pf <- simul(nodes = nodes, model.freq = mf, model.sev = ms, weights = wijt)
信度理论(Credibility Theory)
信度理论一般在预测理赔发生率的时候使用,使用信度理论可以帮助我们把不同的预测结果结合起来。 在层次模型中,我们把一个风险异质化的保险团体分成了很多个风险更加相似的小团体。每个小团体的保费可以用小团体的均值和整个保险团体的均值加权平均来计算。
Actuar包支持四种信度模型 - the unidimensional models of Bühlmann (1969) and Bühlmann and Straub (1970) - the hierarchical model of Jewell (1975) - the regression model of Hachemeister (1975) - linear Bayes models
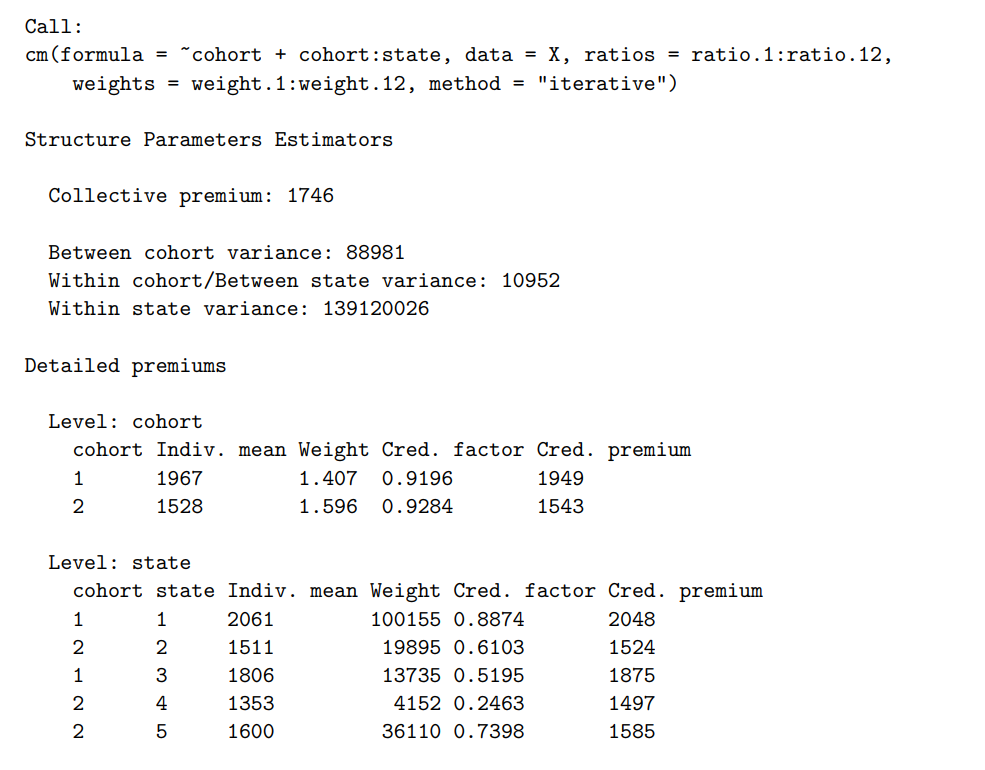
这里重点介绍一下层次模型。在下面的例子中,我们根据cohort和state这两个特征来把大团体分成不同的小团体。 注:ratio.1到ratio.12在这个数据集中代表12个季度内理赔的发生率,Weight是这12个季度在计算保费中的权重 cohort是为了说明的需要多加的一列。代表每行数据属于哪个cohort。hachemeister是我们用的基础数据集。
1 | X <- cbind(cohort = c(1, 2, 1, 2, 2), hachemeister) |
cm的语法解释如下: - ~cohort + cohort:state, :代表层次结构 - data = X, :用的数据集 - ratios = ratio.1:ratio.12, :表示理赔发生率的列 - weights = weight.1:weight.12,:表示权重的列 - method = "iterative":信度保费的计算方式。这个包支持三种计算方式: - the unbiased estimators of Buhlmann and Gisler ¨ (2005) (默认方法) - Ohlsson在2005年提出的一个稍微不同的计算方法 - iterative方法
结果如下,Detailed premiums这个部分可以看每个小团体的信度保费。可以看到 \[ Cred.Premium = Indiv.mean \times Cred.factor + Collective \,\, premium \times (1-Cred.factor) \]