西浦MTH217真题分析(寿险精算)

Jackie

发布于：2022年12月31日

西交利物浦 MTH217 寿险精算I 2019-2020 MTH217 Final Exam涉及的考点分析。

时间过得很快，Jackie辅导西交利物浦大学的MTH217寿险精算I已经是第三届了(辅导课程介绍见《西浦MTH217 / 利物浦MTH273（寿险精算I）考前冲刺课程》)。发现来咨询辅导的同学有个共性的问题，是不知道自己已经自学完成的内容和考试要求的知识点还相差哪些考点。所以今天给大家分析一下2019-2020 MTH217 Final Exam涉及的考点，帮助大家对考试难度有个大致的把握。2022年开始西浦MTH217的老师从杨麟老师换成了白龙老师（也是20级的利息理论的老师），考试风格和往年真题相比可能会有一定程度的变化，但因为仍要满足英国精算师协会对免试认证出题的要求，因此变动不会太大，往年真题仍然可以作为重要的复习资料。

Q1

以往杨麟老师通常会按照第三版《Actuarial Mathematics for Life contingent Risks》（AMLCR textbook）的第一章Introduction to life and long-term health insurance来出一道文字题，考察对寿险精算常识的理解。

除了本题可参考AMLCR外，其余题型在复习时建议全部参考 IFoA英国精算师考试 CM1 科目(对应2019年改革前的CT5寿险精算科目)的官方教材 CMP，CM1科目各章节知识点的具体介绍见《【CM1导引篇】Actuarial Mathematics》.

Q2

对应章节：第 17 章 The life table (生命表)。注：本文使用的章节标题为《CM1 利息理论和寿险精算一对一在线辅导课程介绍》中精算后花园配套讲义目录的标题。

Q2考察Uniform distribution of deaths assumption(UDD)假设下，非整数年龄生存概率和死亡概率的近似。

另外，Constant force of mortality assumption (CFM)假设下，非整数年龄生存概率和死亡概率的近似也需要熟练掌握。

此类题型理解难度不大，但注意总结不同假设下分别如何计算最快捷，选用不同的计算方法，计算速度差异很大。繁琐的方法容易出现计算失误，即便写对也会浪费大量时间。

Q3

对应章节：第 16 章 Survival models (生存模型)。

Q3考察用死亡力(force of mortality) \(\mu_{x}\) 计算对应的生存概率。会使用简单的微积分即可。

本章的公式较多，\(T_0\) 的分布、\(T_x\) 的分布（cdf, sf, pdf）、\(K_x\) 的分布、死亡力与生死概率的关系式、\(T_x\) 和 \(K_x\) 的期望均需要熟练掌握。除了会单独出考题外，本章也是后续章节的基础。

Q5

对应章节：第 18 章 Life assurance contracts (寿险合同)。

Q5考察计算寿险的现值随机变量的期望和方差。本题不是一个保额固定的终身寿险，因此需要掌握各类寿险的的现值随机变量的期望和方差的计算，包括终身寿险（Whole life assurance）、定期寿险（Term assurance）、生存保险（Pure endowment）、生死两全保险（Endowment assurance）和各类寿险延期（Deferred）的形式。现值随机变量的期望的计算贯穿寿险精算整门课，在后续保费和准备金的计算时会频繁用到。而现值随机变量的方差的计算一般只在本章单独进行考察，如果用原始定义式进行求解会相当繁琐，使用快捷方法进行计算可以大大提高计算速度和准确度。

除了寿险外，也需要掌握年金的现值随机变量的期望和方差的计算，对应第 19 章 Life annuity contracts (年金合同) 的内容。

Q6

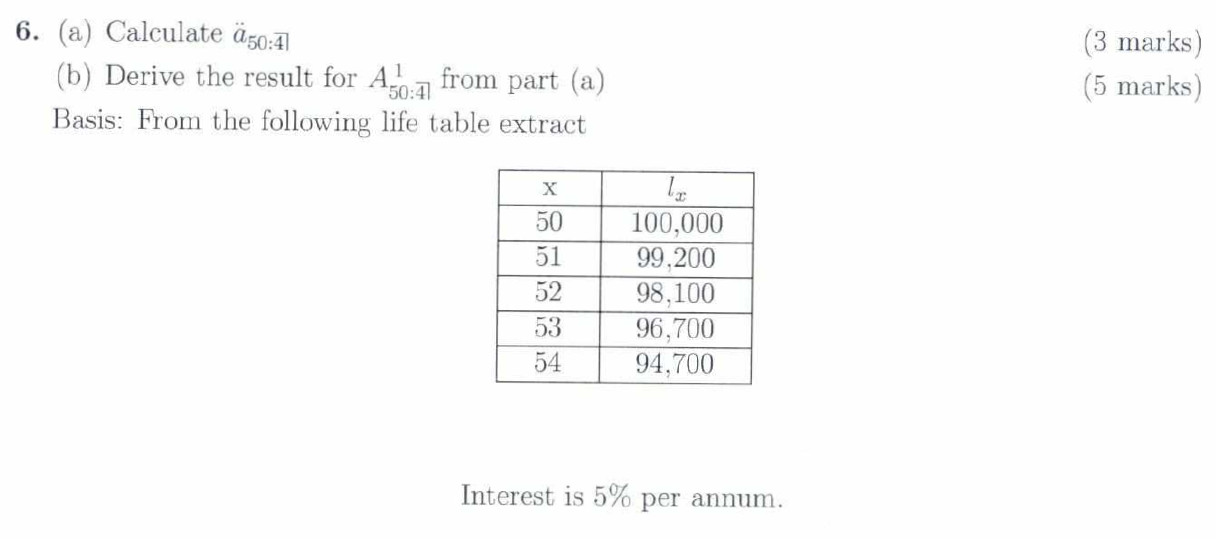
对应章节：第 19 章 Life annuity contracts (年金合同) 和第 20 章 Evaluation of assurances and annuities (寿险和年金EPV的评估)。

Q6(a)给出生命表函数\(l_x\), 显然是需要用生存年金的求和式计算期望现值。而在Q6(a)已经计算生存年金期望现值的前提下，Q6(b)要求计算寿险的期望现值，采用保费换算公式 (Premium conversion formulae) 即可。

本章还需要掌握每年支付 \(m\) 次的生存年金的期望现值的近似计算。

Q7

对应章节：第 22 章 Gross premiums (总保费) 和第 23 章 Gross premium reserves (总保费准备金)。

Q7考察终身寿险的均衡年保费和总保费准备金的计算，是典型题型。同时也考察了未来损失随机变量(Future loss random variable)的书写。

Q8

对应章节：第 21 章 Variable benefits and conventional with-profits policies (可变的保险金和传统分红险) 和第 22 章 Gross premiums (总保费) 和第 24 章复利分红险和保费返还问题。

Q8(a)考察了对各类险种具体保障责任的理解。第一部分的生存年金显然保障的是生存风险；第二部分比较有意思，大家可以思考一下，在什么场景下，客户会需要一个递减型的定期寿险。

Q8(b)考察分红险的均衡月保费的计算。这道题对可变保险金的考察非常全面，同时考察了单利递增的生存年金，单利递减的定期寿险，复利递增的年金和复利递增的寿险。本题考察的复利递增的情况并不是相对简单的 \(1.92308\%\) 的情形，而是相对较难的利率和红利率相等的情形，因此需要对复利递增以及前面章节的期望现值知识点有更为深刻的理解。