涉及的知识点为 CT6 Decision-theory 决策理论
前言
夏令营的英文面里,我被老师问了一个问题:
“Say something about your girlfriend.”
这种出其不意的问题就像蓝天白云晴空万里突然暴风雨。真是难倒我了,巧妇难为无米之炊啊。要不我唱首歌缓解一下尴尬的气氛?
情感问题果然是拉近人们距离的永恒的话题。再严肃的场合,只要问一句“谈朋友了没?”空气里就能立时充满愉快的气氛。
不过其实稍加思索,万能的答题模板总是有的。比如说:
“Actuaries always make assumptions before they solve questions. So I may assume that my girlfriend exists first.”
然后愉快地编一个可爱善良单纯的女生莫名其妙爱上自己的故事。
然而破产概率的调节系数存在的必要条件是个体损失X的矩母函数存在,而厚尾分布的MGF是不存在的。没错,我又用了一回MGF的梗,梗的出处见《恋爱险的起源》。
当然也可以这样说:
“I don't have girlfriend now,but maybe I will find one here during the period of master degree study.”
第二种回答方法需要承担一定的风险。为使自己学校的姑娘免遭祸害,老师可能会拒绝给你优秀营员。别说女朋友了,书都没得读,这就又是另一个悲伤的故事了。

所以最稳妥的做法是赶在老师提问之前找一个女朋友。今后编起故事来也能够得心应手,不至于出现太多破绽。
有女朋友的前提是要先表白。这可不,七夕快要到了,表白的良机啊!
作为一个单身友好型的公众号,精算后花园对粉丝们的终身大事自然不能坐视不理。
但由朋友迈向恋人,既要靠彼此的怦然心动,也得考虑到命运的行程。贸然表白是不理智的。因为求之不得与得而复失,两者都可能成为这项决策的副产品。
所以请千万别着急。我们先来推演两种场景感受一下。
- 可以选择不表白。
心里会出现一个声音:我才二十岁,我还年轻。找对象?先放一放吧。放着放着,就忘了。。。(摊手)

- 如果表白呢?
你忐忑不安地等在大厅里,远远看到喜欢的姑娘在1号窗口,窗口上贴着“表白业务”四个大字。大厅里的广播响了:“请007号到1号窗口。”那位姑娘端坐在窗口里,耐心地听你讲明来意,然后递给你一张好人卡,隔着钢化玻璃客客气气地对你说道:“先生您的卡,请收好。记得给五星好评喔。”附带一个24小时职业化的微笑。她的好人卡发得如此熟练,像是套用了某个现成的模板。你接过来仔细瞧了瞧,千篇一律毫无特色,显然是批量生产的。你转身走出门,隐隐约约听到她在里面说:“下一位。”
这是魔幻现实主义的说法。事实是,无形的好人卡杀伤力远比有形的好人卡强。说起来还真有点扎心。(《巴扎黑经典语录》,孙笑川,2016)相比之下,该说哪个更不幸呢?
所以表白与否的确是一件纠结的事情。有没有那么一种方法,能够帮助你解决这个问题呢?!有啊!那就是决策理论。
根据《美国大百科全书》的“Decision Theory”一条,“所谓做决策,就是在若干个可能的备选方案中进行选择,决策理论则是为了对制定决策的过程进行描述并使之合理化而发展起来的范围很广的概念和方法。”
巧的是,夏令营的笔试部分也考了一道决策理论的题目:
投资者有100万本金,,面临两种选择投资选择:第一种是bond,有固定的4%的收益率;第二种是stock,50%的可能收入10万,40%可能收入5万,10%可能亏损1万。在minimax和bayesian decision criterion下,问分别应该选哪个方案?
今天精算后花园就给大家讲讲 CT6-01-Decision Theory 决策理论。
1.Zero-sum two-player games 双方零和博弈
我们的研究范围是两个玩家(玩家A和玩家B)的零和博弈。即:一方的收益必然意味着另一方的损失,博弈双方的收益和损失相加总和永远为"零"。玩家A和玩家B都有几种不同的策略,把双方策略的不同情况组合起来,可以列出一个矩阵,我们称之为策略矩阵,用来表示博弈的情况。把玩家A的策略编号为I,II,III,…把玩家B的策略编号为1,2,3,…下图是一个2*2的策略矩阵的例子:
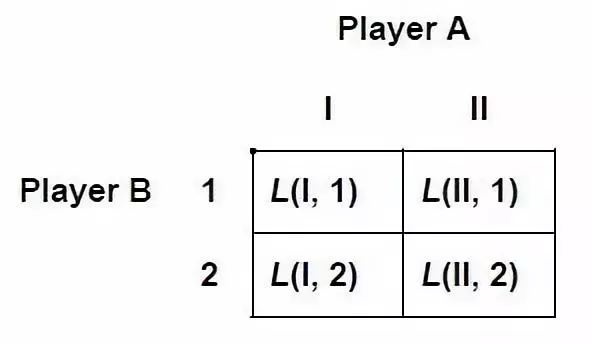
矩阵中的元素称为收益(payoffs)(即玩家A的loss,或者说是玩家B的gain)一般来说,我们称a gain to player B为一个正的payoff。L(I,1)表示当玩家A选策略I,玩家B选策略1时,玩家B的利得。顺便提一下,
1.1 Domination 占优
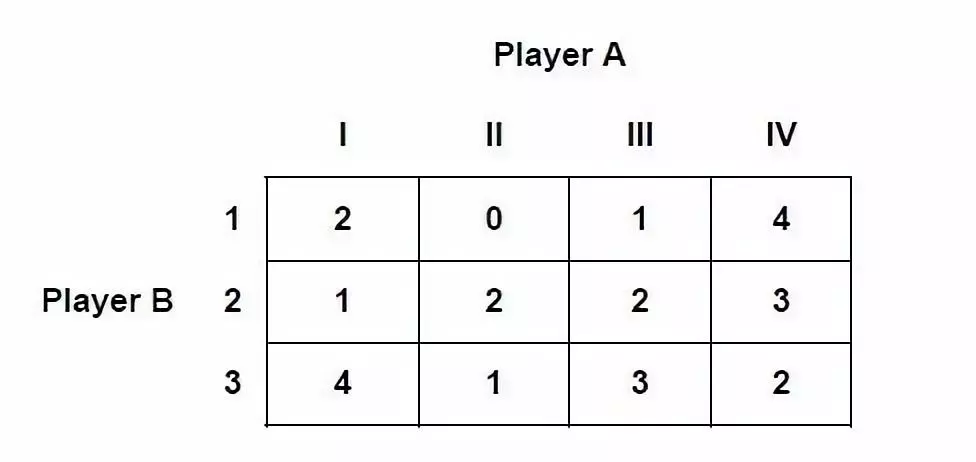
我们来看上图。
策略II dominate
策略IV(II对IV占优),因为II中玩家A的损失总小于IV中的,那么,被占优的(dominated)策略IV(劣势策略)就可以被抛弃了。策略3
dominate 策略1,因为策略3中玩家B的利得总大于策略1中的。同样地,策略II
dominate
策略III。理性的个体永远都不会采取一个被其他策略占优的策略,所以可以把被占优的那些行和列都划掉。如下图:
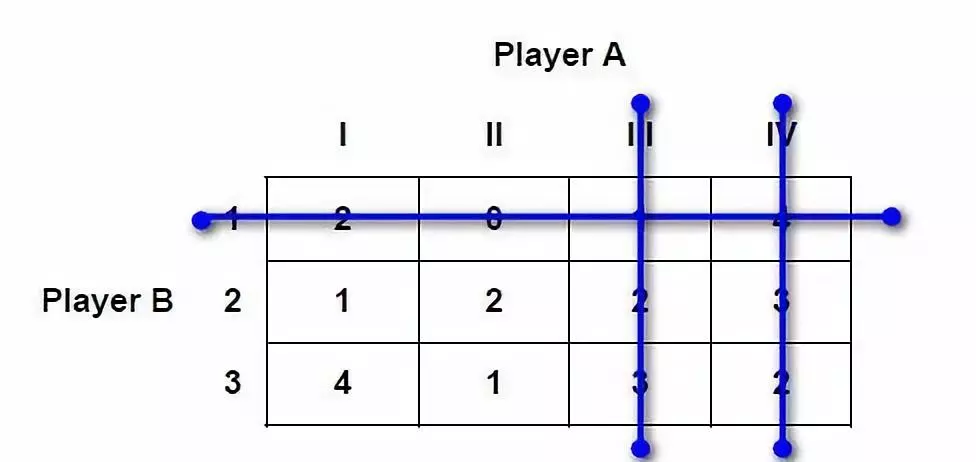
1.2 The Minimax criterion 最小最大法则
顾名思义,最小最大法则就是:使最大损失最小化,或使最小收益最大化。
因为每一列都是玩家A的损失,所以在每列中找出最大数,找出各列中最小的一个。因为每一行都是玩家B的利得,所以在每行中找出最小数,找出各行中最大的一个。这就是所谓的”least worst“。我们来看个例子。
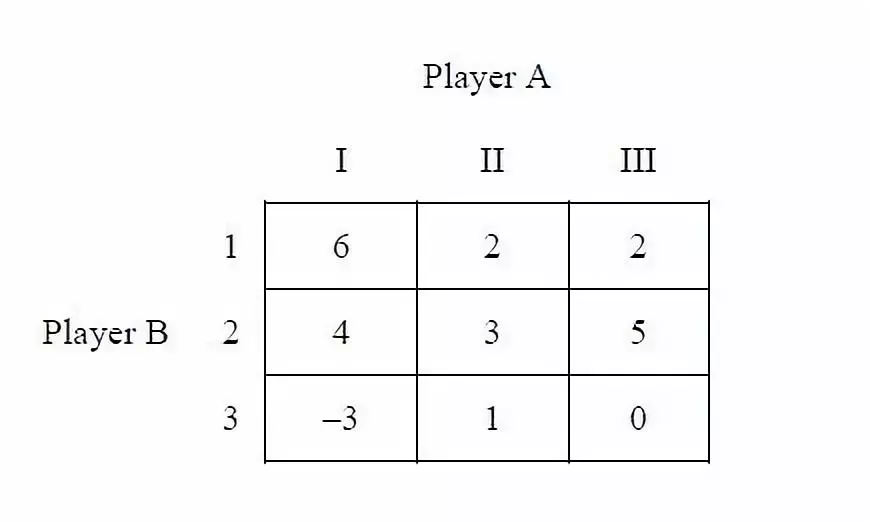
先分析玩家A的minimax strategy:
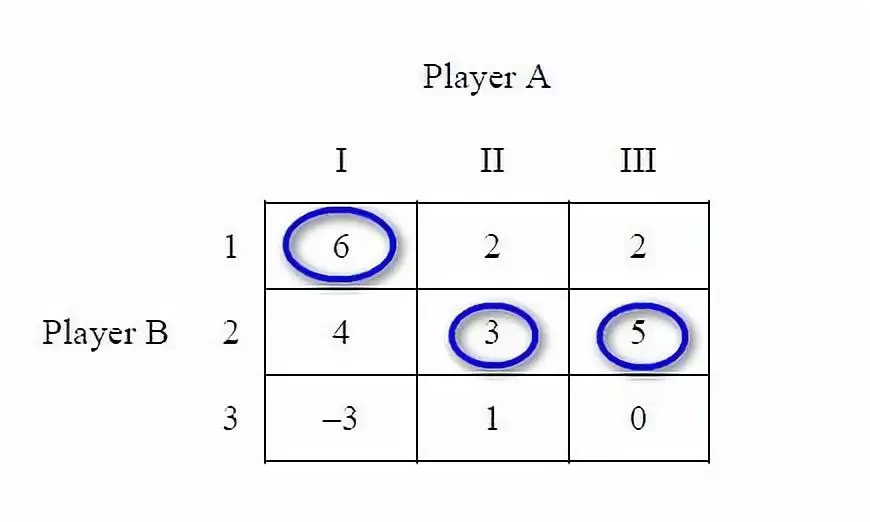
玩家A在策略I,II,III下的最大损失分别为6,3,5。显然3是三者中最小的。所以玩家A的minimax strategy为策略II。
再分析玩家B的minimax strategy:
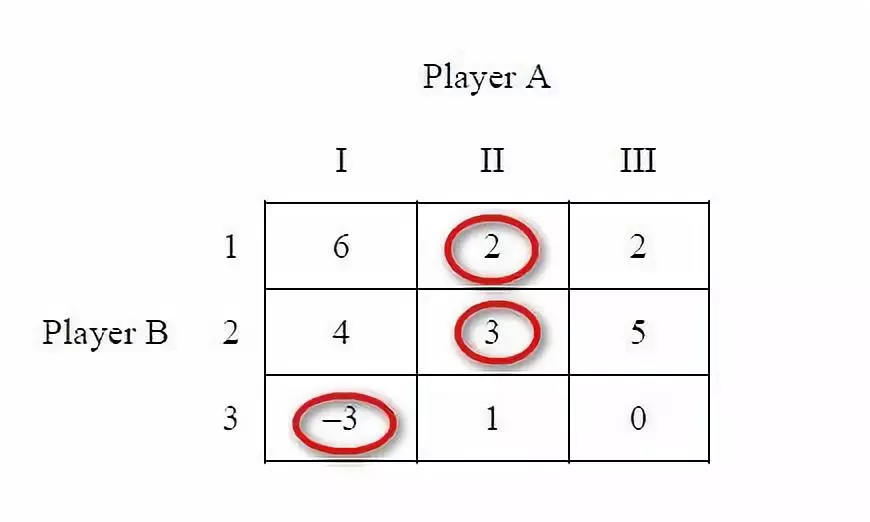
玩家B在策略1,2,3下的最小利得分别为2,3,-3。显然3是三者中最大的。所以玩家B的minimax strategy为策略2。
所以L(II,2)(Row 2, Column 2的点)对玩家A和B来说都是最优的(optimal)策略,即均衡位置(equilibrium position)。这样的点称为鞍点(saddle points)。当鞍点存在时,minimax strategy是”spy-off“的,即:即便双方互相知晓对方的决策,也不影响他们自己最后做出的决策。决策点最终还是会落在均衡位置(鞍点)上。
1.3 Randomised Strategies 随机化策略
若鞍点不存在,那么minimax strategy就不是”spy-off“的,当我们知道对手的决策时,我们就可以采取相应的措施。这时我们可以使用Randomised Strategies:一个玩家的策略是关于对手策略的函数时,玩家如何采取策略,使得最大损失最小化。
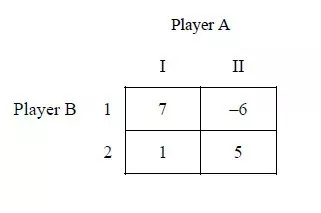
上图的例子不存在鞍点。所以我们应该采取随机化策略。
记采取策略I的概率为p,则采取策略II的概率为1-p。
若玩家B采取策略1,玩家A的期望损失L1( p)=7p -6(1-p) =13p-6。若玩家B采取策略2,玩家A的期望损失L2( p)=p +5(1-p) =5-4p。我们要求的是能使得两者中的较大损失最小的p。显然令两者相等,13p-6=5-4p,求出p即可。
2.Statistical games 统计博弈
统计推断(statistical inference)可以视作Nature(自然)和statistician(统计学家)之间的博弈。在统计博弈中,统计学家有一些样本数据,这些数据可以给出一些关于Nature的选择的信息(information about Nature‘s choice)。
Example: 一个统计学家被告知有两种硬币:一种是a head and a tail(一面是head,另一面是tail);另一种是two heads(两面都是head)。他要根据一次投掷后观察的硬币的其中一面来判断自己面前的硬币是哪一种。判断错误罚1块钱,判断正确不赏也不罚。
先忽略统计学家可以观测到一次投掷的信息,可以把上述问题看作以下博弈:
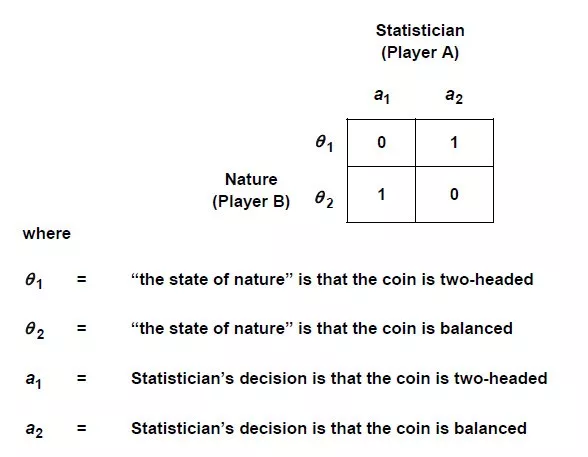
但实际上统计学家可以观测到一次投掷的硬币信息。记x=0为观测到head,x=1为观测到tail。
决策函数(decision function)可以为:
\[d_{1}(x)=\left\{\begin{array}{l} a_{1} \text { when } x=0 \\ a_{2} \text { when } x=1 \end{array}\right.\]
上述决策函数也可记为:d1(0) =a1 and d1(1)=a2。当然决策函数还可以用别的。再写三个:
- d2(0) =a1 and d2(1) =a1; - d3(0) =a2 and d3(1) =a2; - d4(0) =a2 and
d4(1) =a1。
上述表格里的元素即为损失函数loss function,一般化可写为:

上述决策函数d1(x)的期望损失:
\[R\left(d_{1}, \theta_{j}\right)=E\left[L\left(d_{1}(x), \theta_{j}\right)\right]\]
等式右边的中括号里面的就是采用决策函数d1(x)时的损失函数。
R称为风险函数Risk function,为期望损失。要计算出这些损失的期望,需要知道各损失函数的概率。
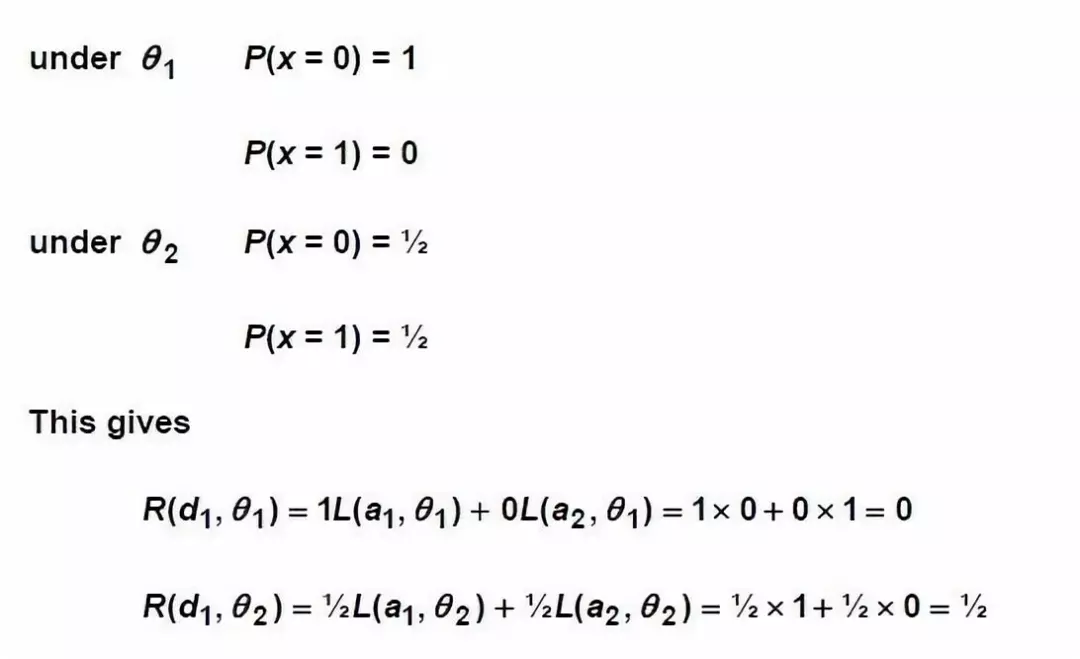
同样地,可以计算出其他三个决策函数下的期望损失,从而得到以下矩阵:
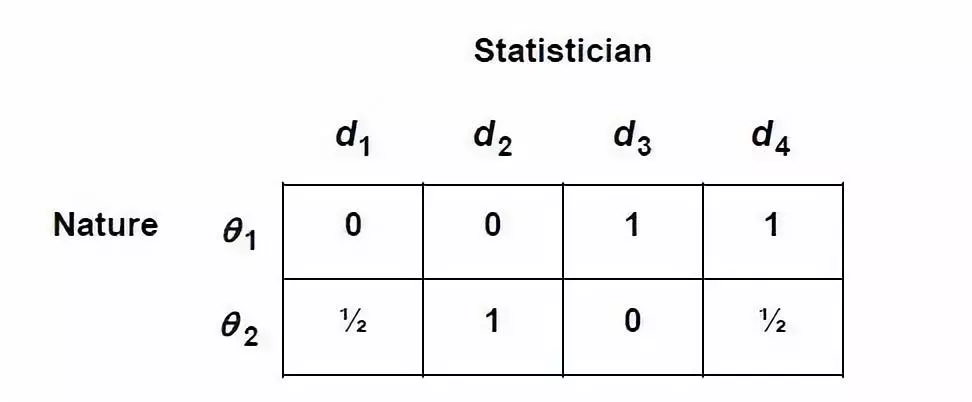
- d1 dominates d2;
- d3 dominates d4。 此时鞍点不存在,所以我们可以用随机化策略确定最优策略:采取决策函数d1和d3的概率分别为2/3和1/3(用上文的方法自己算一下吧)。
3.Decision criteria 决策法则
3.1 The minimax criterion 最小最大法则
根据最小最大法则选择决策函数d即可。
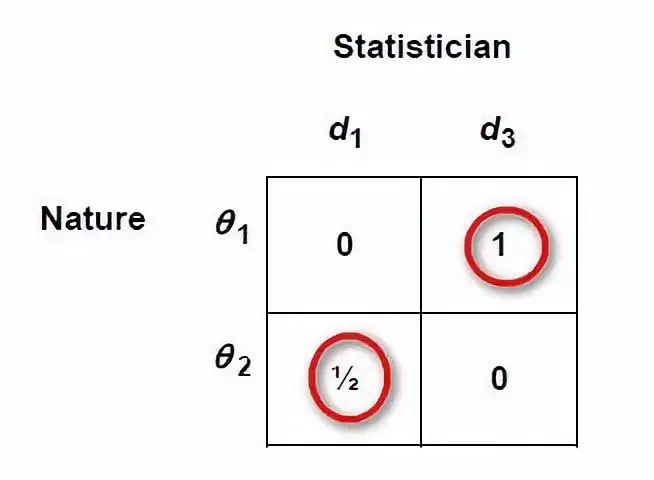
显然对于刚才的例子,应选择d1。
3.2 The Bayes criterion 贝叶斯法则
当我们把Theta视作随机变量,就可以根据贝叶斯法则来选择决策函数。Theta是有一定的概率分布的。例如:

当p>1/3,d1下的Bayes risk比d2小,选择d1;当p<1/3,d2下的Bayes risk比d1小,选择d2;当p=1/3,两者相同,选哪个都一样。
结语
以上就是决策理论的全部内容。
回到我们最开始的问题:表白与否,答案究竟是什么?
要是有标准答案,那也不叫围城了。
当然,如果七夕那天喜欢的女孩子正好来找你聊天,那表白就容易多了。——“学校东门外新开了一家店好像不错诶。”——“知道了,我也喜欢你。”