1支雪糕引发的“糕利贷”

Jackie

发布于：2022年7月3日

人生就像一个冰柜，你永远不知道下一支雪糕要分多少期。

夏日的午后，气温攀升。刚排队做完核酸的 Jackie 不堪酷暑，来到路边的便利店买了一支不知名的雪糕。结账时才发现，居然要 19.82 元！

百闻不如一见，我终于领略到了什么叫做“雪糕刺客”：冰柜里其貌不扬的一支雪糕，却用高不可攀的价格狠狠刺痛了我。一口下去，好几块钱就没了。

今天出门着急，没带现金。看着空空如也的钱包，我不禁陷入了沉思。正如电影《阿糕正传》所说：人生就像一个冰柜，你永远不知道拿一支雪糕多少钱。更要命的是，昨天刚交完房租，做精算这点微薄的工资还没捂热就全贡献给房东了，支付宝余额里也没有钱。

便利店的老板似乎看出了我的窘境，指着墙上的二维码说：本店支持花呗支付。

我赶紧掏出手机，选了花呗分期12期：

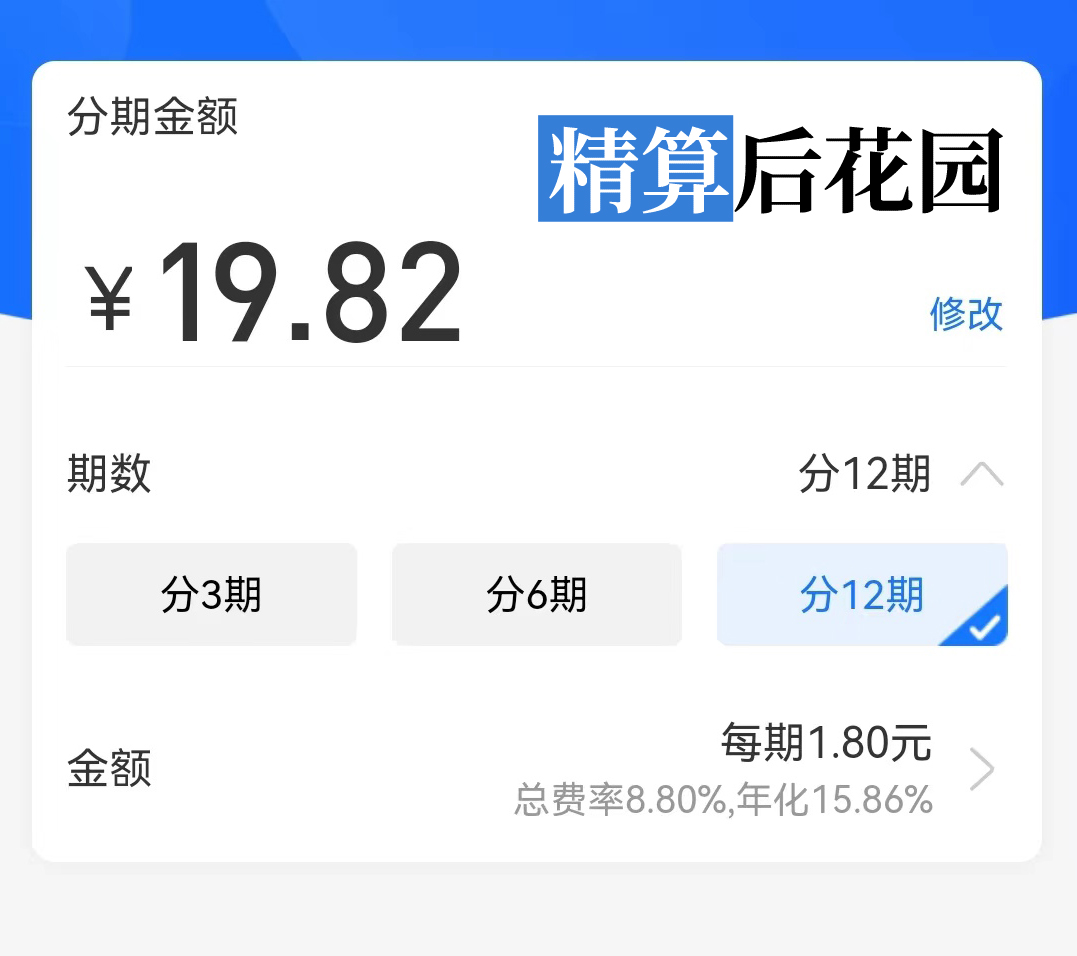
可以看到：

在手续费率为 \(8.8\%\) 的情况下，将 19.82 元分 12 期偿还，每期的还款额为 1.80 元。

这个手续费是怎么算的？点开详情看一下说明：

分期总手续费 \(=\) 本金 \(\times\) 分期总手续费率 \(=19.82 \times 8.8\%\).

所以按照等额本息法还款，每期的还款额 \(=19.82 \times (1+8.8\%) \div 12 \approx 1.797\). 验算无误。

这里 \(8.8\%\) 的总手续费率是不是我们平时讲的年利率呢？

不是的。为什么说不是呢？我们可以简单地想一下。如果本金一直是 19.82 元，那么这里的 \(8.8\%\) 一直作用于初始的本金，计算出来的年利率就应该是 \(8.8\%\). 但是由于我们在12期的整个还款过程中，每期还款后，剩余未偿还本金会越来越少，所以实际的年利率必然比 \(8.8\%\) 高。大致估算一下，假定本金在偿还过程中线性减少到零为止，也就是说整个还款期里平均的本金是初始本金的一半，对应的年利率大约是年手续费率的两倍，约 \(8.8\% \times 2 =17.6\%\).

实际上，分期12期（每期为1月）的总手续费率就是我们在 IFoA 英国精算师考试的 CM1 : Actuarial Mathematics 科目 Chapter 10 Loan schedules中讲的 Flat rate of interest. 我们可以借助 flat rate 的两倍（略小一些）来粗略估计年利率(Annual Percentage Rate of charge, or APR)。

当然，作为一名精算师，我们不能只满足于粗算。接下来我们来精确计算分期12期对应的年利率。

列出价值等式，令每期还款额的现值（以月利率 \(j\) 贴现）等于本金 19.82 元： \[ 1.797 \times a_{\mkern1mu\overline{12\,}\kern-3mu\lower-1mu\small|@j} = 19.82 \]

可以解出月利率 \(j=1.322\%\). 这里用到的就是保险代理人在销售储蓄型险种时经常说的内部收益率（internal rate of return, IRR）计算方法。

按照支付宝的手续费说明，年化利率按单利计算： \(i=12\times 1.322\% \approx 15.86\%\). 验算无误。

注意，如果年化利率按照复利计算： \(i=(1+1.322\%)^{12}-1 \approx 17.07\%\). 这样的年化贷款利率是相当高昂的。

我们可以用卡西欧金融计算器 FC-200V 或 FC-100V 计算上述的月利率：

首先，按下 CMPD, 进入 CMPD 复利计算模式。接着设定各个参数：

Set:End 用于设定年金是期初支付还是期末支付。这里我们要使用的是期末年金，无需更改。（如果要使用期初年金，则依次按下 EXE \(\rightarrow\) 2，屏幕会显示为 Set:Begin ）;
N 为付款次数（期数）（Number of Periods）. 使用向下的方向键 \(\blacktriangledown\) 选取 N ，输入数值 12，按下 EXE 确认;
I% 为每期利率的100倍（effective interest rate in percentage）. 本题的价值等式中每期利率是我们要求解的值，所以不预先设定利率值，暂时跳过;
PV 为现值（Present Value）. 使用向下的方向键 \(\blacktriangledown\) 选取 PV ，依次输入 (-) \(\rightarrow\) 19.82，按下 EXE 确认。注意：计算器的内置程序默认现值为流出的现金流，所以输入现值时需要加负号;
PMT 为年金每期付款额（Payment）. 使用向下的方向键 \(\blacktriangledown\) 选取 PMT ，输入数值 1.797，按下 EXE 确认;
FV 为终值（积累值）（Future Value）. 本题的价值等式中用不到终值，所以直接跳过;
P/Y 为年付款数. C/Y 为年复利数，本题用不到，直接跳过.
最后，使用向上的方向键 \(\blacktriangle\) 选取 I%，按下 SOLVE 进行求解即可。结果显示 I% = 1.321908668，验算无误。

银行的信用卡分期折算年化费率（即单利年化利率）也可以用内部收益率法求解。给大家看一个例子：

列出价值等式，令每期还款额的现值（以月利率 \(j\) 贴现）等于本金 449.04 元： \[ 44.46 v_j + 39.13 v_j^2 + \ldots + 39.13 v_j^{12} = 449.04 \]

这里银行可能出于凑整的目的，首期的后续每期的还款额不相等，所以我们不能用 CMPD 复利计算模式，而要用 CASH 现金流量模式。

按下 CASH, 进入 CASH 现金流量模式。接着设定各个参数：

I% 为每期利率的100倍（effective interest rate in percentage）. 本题的价值等式中每期利率是我们要求解的值，所以不预先设定利率。因为 I% 里已经储存了上一题计算出的结果，我们输入数值 0，按下 EXE 确认，以清空 I% 中存储的值;
使用向下的方向键 \(\blacktriangledown\) 选取 Csh=D.Editor x, 然后按下 EXE 进入现金流编辑界面。注意，现金流编辑界面的第1行是0时刻：我们将0时刻作为流出的现金流，依次输入 (-) \(\rightarrow\) 19.82，按下 EXE 确认; 第2行是1时刻，输入 44.46，按下 EXE 确认; 第3行是2时刻，输入 39.13，按下 EXE 确认; 以此类推，在第4-13行均输入 39.13，按下 EXE 确认。输入完毕后，按下 ESC 返回 CASH 现金流量模式的主屏幕。
最后，使用向下的方向键 \(\blacktriangledown\) 选取 IRR: Solve, 按下 SOLVE 进行求解即可。结果显示 IRR = 0.880435564.