梦里也能见到她，你大概是喜欢这个姑娘：从贝叶斯到极大似然估计
涉及的知识点为贝叶斯和极大似然估计。
本文的目的是让没有学过贝叶斯公式的同学对贝叶斯公式有个具体生动的印象。已经掌握得很好的同学可以略过这篇文章。限于作者水平，面面俱到是不可能的，这句话也同样适用于本公众号的其他文章。毕竟孙子也说过，备前则后寡，备左则右寡，无所不备，则无所不寡。
场景假定
我们设想一个场景：某个晚上，Jackie梦见了一个姑娘。
这件事情显然可以有两种可能性：
- 其一，Jackie喜欢这个姑娘，因此寤寐思服。
- 其二，Jackie不喜欢这个姑娘，梦见她纯属偶然。
我们把事件“Jackie梦见这个姑娘”记作B1；把事件“Jackie没有梦见这个姑娘”记作B2;把事件“Jackie喜欢这个姑娘”记作A1；把事件“Jackie不喜欢这个姑娘”记作A2。
设定各事件的概率
为了让这个场景更加生动，作者决定写一段话解释各事件的概率是如何设（Xia）定(Bai)的。
因为这个姑娘还有些漂亮，不妨假定“Jackie喜欢这个姑娘”的概率为0.6，略高于“Jackie不喜欢这个姑娘”的概率0.4。
又因为Jackie在武汉某所“男女三比七”的财经类院校就读，而作为本文作者，Jackie显然是一个专情的人，如果喜欢一个姑娘，只要梦见女生，梦见的就一定是这位姑娘，所以“Jackie喜欢这个姑娘的前提下梦见这个姑娘”的概率大致为0.7；如果不喜欢这个姑娘呢，梦见她的概率和梦见男生的概率差不多，为0.3。
我们可以画出以下树状图：
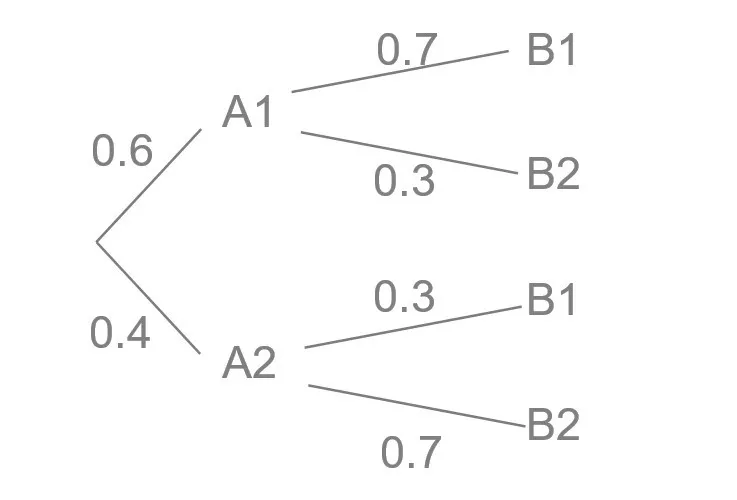
计算条件概率
Jackie在各情形下梦见这个姑娘的概率：
\[P\left(B_{1}\right)=0.6 * 0.7+0.4 * 0.3=0.54\]
Jackie喜欢并且梦见这个姑娘的概率：
\[P\left(A_{1} B_{1}\right)=0.6 * 0.7=0.42\]
给定梦见的前提，Jackie喜欢该姑娘的条件概率：
\[P\left(A_{1} | B_{1}\right)=\frac{P\left(A_{1} B_{1}\right)}{P\left(B_{1}\right)}=\frac{7}{9}\]
同样地，给定梦见的前提，Jackie不喜欢该姑娘的条件概率：
\[P\left(A_{2} | B_{1}\right)=\frac{P\left(A_{2} B_{1}\right)}{P\left(B_{1}\right)}=\frac{2}{9}\]
显然前者更大。所以说，会在梦里遇到她，大概潜意识就是很喜欢这个姑娘了。证毕。
我们计算条件概率时用到的就是贝叶斯公式。
联想到极大似然估计
从上述的例子我们可以发现，“梦见这个姑娘”这个事件最像是发生在“喜欢这个姑娘”的前提下。这个推断是符合人们的经验事实的。
“最像”就是“极大似然”的意思。这就暗含了极大似然估计估计的思想：已经发生的事情，就是最可能会发生的。
严格的说，极大似然估计的目的是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。
习题
看完这个例子，大家对贝叶斯公式的理解有没有更加具体呢？来道习题检验一下吧。这是IFoA2016年4月的第四道真题，也是2017年慕再精算竞赛里的题源之一。
答案如下：
当然，本文离不开一个最重要的前提假设：
首先得有这样一个姑娘存在
重要的事用英文再说一遍：
We may assume that GuNiang exists first.
正在检查 Disqus 能否访问...